Parallel and Perpendicular Axes Theorems

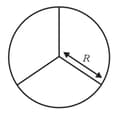
A wheel comprises a ring of radius $R$ and mass $M$ and three spokes of mass $m$ each. The moment of inertia of the wheel about its axis is

If $I_1$ is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and $I_2$ is the moment of inertia of the ring about an axis perpendicular to plane of ring and passing through its centre formed by bending the rod, then

The ratio of the radii of gyration of a circular disc about a tangential axis in the plane of the disc and of a circular ring of the same radius about a tangential axis in the plane of the ring is,

A solid sphere of radius $R$ has a moment of inertia $I$ about its geometrical axis. If it is melted into a disc of radius $r$ and thickness $t$. If it's moment of inertia about the tangential axis (which is perpendicular to the plane of the disc), is also equal to $I$, then the value of $r$ is equal to

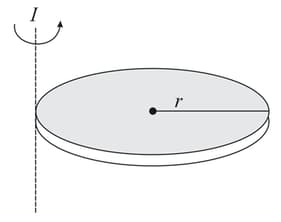
A hollow cylinder has mass $M$, outside radius $R_2$ and inside radius $R_1$. Its moment of inertia about an axis parallel to its symmetry axis and tangential to the outer surface is equal to

A solid sphere of mass $M$ and radius $R$ having moment of inertia $I$ about its diameter is recast into a solid disc of radius $r$ and thickness $t$. The moment of inertia of the disc about an axis passing the edge and perpendicular to the plane remains $I$. Then $R$ and $r$ are related as

Which of the following statements is true in case of the principle of perpendicular axes?

One quarter sector is cut from a uniform circular disk of radius $R$. This sector has a mass $M$. It is made to rotate about a line perpendicular to its plane passing through the center of the original disc. Its moment of inertia about the axis of rotation is,

The moment of inertia of a thin uniform rod of mass $M$ and length $L$ about an axis perpendicular to the rod through its centre is $I$. The moment of inertia of the rod about an axis perpendicular to the rod through its end point is

From a disc of radius $R$, a concentric circular portion of the radius $r$ is cut out so as to leave an annular disc of mass $M$. The moment of inertia of this annular disc about the axis perpendicular to its plane and passing through its centre of gravity is