Law of Radioactive Decay

The count rate of a radioactive sample was $1600 \mathrm{count} {\mathrm{s}}^{–1}$ at $t=0$ and $100 \mathrm{count} {\mathrm{s}}^{–1}$ at $t=8 \mathrm{s}.$ Select the correct alternatives

Radioactive nuclei are being generated at a constant rate by some kind of nuclear reaction. If the decay constant for the radioactive nuclei is $\mathrm{\lambda }$, which of the following graphical representation is correct? (initially, there are no radioactive nuclei present)

The decay constant of a radioactive substance is $\lambda$. At $t=0$, the number of active nuclei are $N_0$. Select the correct alternative

Disintegration consicrit of a radioactive material is $\mathrm{\lambda }$

In a sample of ${}_{86}{}^{211}\mathrm{Rn}$ nuclei, 25 percent decay by $\alpha$ -decay to ${}_{84}{}^{207}\mathrm{Po}$ and the rest decay by electron capture to ${}_{85}{}^{211}\mathrm{At}$. What is the ratio of the mean life for $\alpha$ -decay, ${\tau }_{\alpha }$, to the mean life for electron capture, ${\tau }_{\beta }?$

Mean life of a radioactive substance is 1620 and 2160 years for $\alpha$ and $\beta$ emission respectively. At any instant $\alpha$ particles are emitted at a rate of $4\times {10}^5{ \mathrm{s}}^{-1}$ and $\beta$ particles at $3\times {10}^5{ \mathrm{s}}^{-1}.$ Mass number of substance is $234$ and take time for $1$ year as $3\times {10}^7 \sec .$ If mass of radioactive substance at that instant is $\mathrm{x}\times {10}^{-6} \mathrm{gm}$ find $x$ (Take Avogadro no. $=6\times {10}^{23}$) (Approximate the answer to the nearest integer.)

Two radioactive nuclei $P$ and $Q$ in a given sample decay into a stable nucleus $R$. At time $t=0$, the number of $P$ species are $4N_0$ and that of $Q$ are $N_0$. Half-life of $P$ (for conversion to $R$) is $1 \mathrm{minute}$ whereas that of $Q$ is $2 \mathrm{minutes}$. Initially, there are no nuclei of $R$ present in the sample. When number of nuclei of $P$ and $Q$ are equal, the number of nuclei of $R$ present in the sample would be,

The activity of a radioactive substance decreased to one-third of the original activity number $N_0$ in a period of $9 \mathrm{yr}$. After a further lapse of $9 \mathrm{yr}$, its activity will be

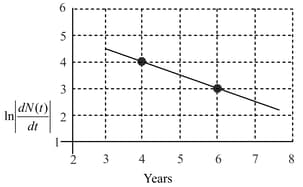
To determine the half life of a radioactive element, a student plots a graph of $\ln \frac{dN\left(t\right)}{dt}$ versus $t.$ Here,  $\frac{dN\left(t\right)}{dt}$ is the rate of radioactive decay at time $t.$ If the number of radioactive nuclei of this element decreases by a factor of $p$ after $4.16$ years, the value of $p$ is:

Nuclei of radioactive element $A$ are produced at rate $t^2$ at any time $t$. The element $A$ has decay constant $\lambda .$ Let $N$ be the number of nuclei of element $A$ at any time $t.$ At time $t=t_0, \frac{\mathit{d}\mathit{N}}{\mathit{d}\mathit{t}}$ is minimum. Then the number of nuclei of element $A$ at time $t=t_0$ is

A radioactive element $X$ converts into another stable element $Y$. Half life of $X$ is $2 \mathrm{hrs}$. Initially only $X$ is present. After time $t$, the ratio of atoms of $X$ and $Y$ is found to be $1: 4$, then $t$ in hours is

A sample of radioactive material decays simultaneously by two processes $A$ and $B$ with half lives $\frac{1}{2}$ and $\frac{1}{4} \mathrm{hr}$, respectively. For first half hour it decays with the process $A\text{,}$ next one $\mathrm{hr}$ with the process $B$ and for further half an hour with both $A$ and $B$. If originally there were $N_0$ nuclei, find the number of nuclei after $2 \mathrm{hr}$ of such decay.

A parent nucleus $X$ undergoes $\alpha -$ decay with a half-life of $75000$ years. The daughter nucleus $Y$ undergoes $\beta -$ decay with a half-life of $9$ months. In a particular sample, it is found that the rate of emission of $\beta -$ particles is nearly constant (over several months) at ${10}^7 {\mathrm{h}}^{-1}.$ What will be the number of $\alpha -$ particles emitted in an hour?

A radioactive substance is being produced at a constant rate ${}^{\text{'}}a^{\text{'}}$ per second. Its decay constant is $b$. The relation between the maximum number of nuclei of $X$ is $N_{\max }=\frac{aK}{b}$, then the value of $K$ is

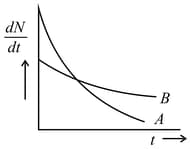
The variation of decay rate of two radioactive samples A and B with time is shown in figure. Which of the following statements are true?

$\frac{7}{8}$ fraction of a sample disintegrates in $t$ time. How much time it will take to disintegrate $\frac{15}{16}$ fraction?

A radioactive sample disintegrates by $10\%$ during one month. How much fraction will disintegrate in four months?

The decay constant of the parent nuclide in Uranium series is $\lambda$. Then, the decay constant of the stable end product of the series will be,

A freshly prepared radioactive source of half-life $2 \mathrm{hr}$ emits radiation of intensity which is $64$ times the permissible safe level. The minimum time after which it would be possible to work safely with this source is,

The activity of a sample of radioactive material is $A_1$ at time $t_1$ and $A_2$ at time $t_2\left(t_2>t_1\right)$ . Its mean life is T. Which of the following is correct?