Embibe Experts Solutions for Chapter: Work, Energy and Power, Exercise 3: Level 3

A body of mass $m$ is rotated in a vertical circle of radius $r$. The minimum velocity of the body at the topmost position for the string to remain just stretched is

A particle of mass $m$ is rotating by means of a string in a vertical circle. The difference in the tension at the bottom and top would be-

A particle rests on the top of a hemisphere of radius $R$. Find the smallest horizontal velocity that must be imparted to the particle if it is to leave the hemisphere without sliding down is

A small body of mass $m$ slides down from the top of a hemisphere of radius $r$. The surface of the block and hemisphere are frictionless.

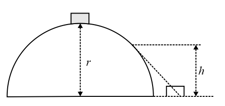
The height at which the body loses contact with the surface of the sphere is

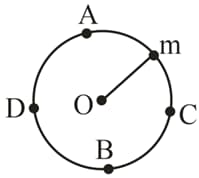
A particle of mass $\mathrm{m}$ is performing vertical circular motion (see figure). If the average speed of the particle is increased, then at which point maximum breaking possibility of the string :-

A heavy particle hanging from a string of length $\ell$ is projected horizontally from equilibrium position with speed $\sqrt{\mathrm{g}\ell }$. The speed of the particle at the point where the tension in the string equals weight of the particle is :-

A particle of mass $m$ is attached at the end $\mathrm{B}$ of uniform rod of same mass $m$ and length $l$. If the rod is whirled in vertical circle about end $\mathrm{A}$. What is minimum speed of particle at end $\mathrm{B}$, required to move it in vertical circle ?

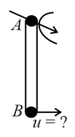
A heavy particle hanging from a string of length $l$ is projected horizontally with speed $\sqrt{\mathrm{g}l}.$ The speed of the particle at the point where the tension in the string equals weight of the particle is: