Newton's Second Law for Rotational Motion

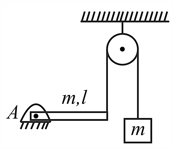
Uniform rod $AB$ is hinged at end $A$ in horizontal position as shown in the figure. The other end is connected to a block through a massless string as shown. The pulley is smooth and massless. Masses of block and rod is same and is equal to $m$. Then acceleration of block just after release from this position is

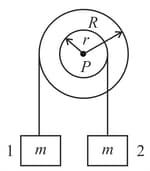
Two blocks each of mass m are hanging from a stepped pulley by an inextensible light string which passes over a stepped pulley. The mass of the pulley is $m$ and its radius of gyration is $k$. If the string does not slide on the pulley, find the accelerations of the blocks.

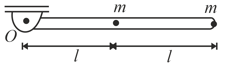
A light rigid rod is connected rigidly with two identical particles each of mass m as shown. The free end of the rod is smoothly pivoted at $O$. The rod is released from rest from its horizontal position at $t=0$. Find:

(i) angular acceleration of the rod, at $t=0$.

(ii) reaction offered by the pivot, at $t=0.$

A disc of mass $m$ and radius $r$ is pivoted smoothly with a block of mass $M.$ A force $F_1$ acts on $m$ and another force $F_2$ acts on $M$. Assume that ground is smooth. Find the:

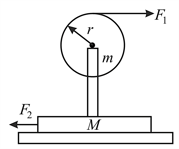
(i) Linear acceleration of the disc.

(ii) angular acceleration of the disc.

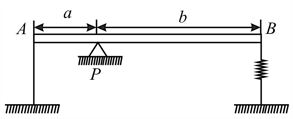
A uniform rod $AB$ of mass $m=2 \mathrm{k}\mathrm{g}$ and length $l=1.0 \mathrm{m}$ is placed on a sharp support $P$ such that $a=0.4 \mathrm{m}$ and $b=0.6 \mathrm{m}$. A spring of force constant $k=600 \mathrm{N} {\mathrm{m}}^{-1}$ is attached to end $B$ as shown in figure. To keep the rod horizontal, its end $A$ is tied with a thread such that the spring is elongated by $1 \mathrm{c}\mathrm{m}$. Calculate reaction of support $P$ when the thread is burnt.

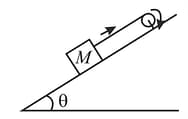
A wheel of radius $r$ and moment of inertia $I$ about its axis is fixed at the top of an inclined plane of inclination $\mathrm{\theta }$ as shown in figure. A string is wrapped around the wheel and its free end supports a block of mass $M$ which can slide on the plane. Initially, the wheel is rotating at a speed $\mathrm{\omega }$ in a direction such that the block slides up the plane. How far will the block move before stopping?

A uniform rod of mass $m$ and length $l$ can rotate in a vertical plane about a smooth horizontal axis hinged at point $H$. Find the force exerted by the hinge just after the rod is released from rest, from an initial horizontal position?

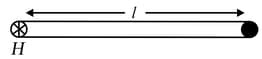
A uniform rod of mass m and length $l$ can rotate in a vertical plane about a smooth horizontal axis hinged at point $H$.

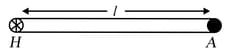
(a) Find angular acceleration $\alpha$ of the rod just after it is released from initial horizontal position from rest?

(b) Calculate the acceleration (tangential and radial) of point $A$ at this moment.

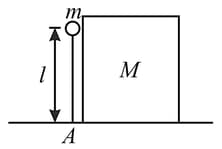
A weightless rod of length $l$ with a small load of mass $m$ at the end is hinged at point $A$ as shown and occupies a strictly vertical position, touching a block of mass $M.$ A light jerk sets the system in motion. For what mass ratio $M/m$ will the rod form an angle $\theta =\pi /6$ with the horizontal at the moment of the separation from the block?

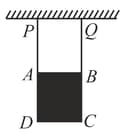
A square plate $ABCD$ of mass $m$ and side $l$ is suspended with the help of two ideal strings $P$ and $Q$ as shown. Determine the acceleration (in $m/{\mathrm{s}}^2$) of corner $A$ of the square just at the moment the string $Q$ is cut. $\left(g=10 \mathrm{m}/{\mathrm{s}}^2\right)$

A uniform rod $AB$ of mass $2 \mathrm{kg}$ is hinged at one end $A.$ The rod is kept in the horizontal position by a massless string tied to point $B.$ Find the reaction of the hinge (in $N$) on end $A$ of the rod at the instant when string is cut. $\left(g=10 \mathrm{m}/{\mathrm{s}}^2\right)$

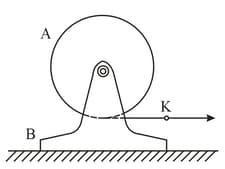
A uniform solid cylinder $A$, of mass $m_1$, can freely rotate about a horizontal axis fixed to a mount $B$, of mass $m_2$. A constant horizontal force $F$, is applied to the end $K$, of a light thread tightly wound on the cylinder. The friction between the mount and the supporting horizontal plane is assumed to be absent. Find: 

$\left(a\right)$ the acceleration of the point $K$
$\left(b\right)$ the kinetic energy of this system, $t \mathrm{seconds}$ after the beginning of motion. 

Two identical discs of mass $m$ and radius $r$ are arranged, as shown in the figure. If $\alpha$ is the angular acceleration of the lower disc and $a_{cm}$ is the linear acceleration of the centre of mass of the lower disc, then the relation between $a_{cm}$, $\alpha$ and $r$ is