Simple Harmonic Motion

The bob of a simple pendulum has a mass of $0.40kg$. The pendulum oscillates with a period of $2.0s$ and an amplitude of $0.15m$.At one point in its cycle it has a potential energy of $0.020$ $J$.What is the kinetic energy of the pendulum bob at this point?

A mass, hung from a spring, oscillates with simple harmonic motion. Which statement is correct?

When a cricket ball hits a cricket bat at high speed it can cause a standing wave to form on the bat. In one such example, the handle of the bat moved with a frequency of 60Hz with an amplitude of 2.8mm. The vibrational movement of the bat handle can be modelled on simple harmonic motion. Calculate the maximum acceleration of the bat handle.

When a cricket ball hits a cricket bat at high speed it can cause a standing wave to form on the bat. In one such example, the handle of the bat moved with a frequency of 60Hz with an amplitude of 2.8mm. The vibrational movement of the bat handle can be modelled on simple harmonic motion. State the conditions for simple harmonic motion.

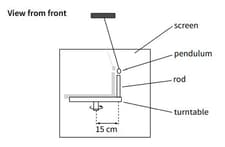
This diagram shows a turntable with a rod attached to it a distance $15 \mathrm{cm}$ From the centre. The turntable is illuminated from the side so that a shadow is cast on a screen.

A simple pendulum is placed behind the turntable and is set oscillating so that it has an amplitude equal to the distance of the rod from the centre of the turntable. The speed of rotation of the turntable is adjusted. When it is rotating at $1.5$ Revolutions per second the shadow of the pendulum and the rod are found to move back and forth across the screen exactly in phase. Explain what is meant by the term in phase.

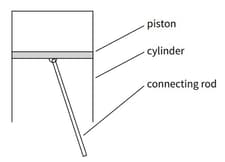
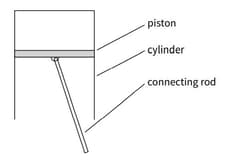
This diagram shows the piston of a small car engine that oscillates in the cylinder with a motion that approximates simple harmonic motion at $4200$ revs per minute $\left(1 rev=1cycle\right).$ The mass of the piston is $0.24kg$

The amplitude of the oscillation is $12.5cm$. Calculate the forces required on the piston to produce the maximum acceleration.

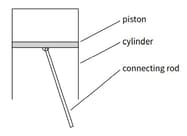
Shows the piston of a small car engine that oscillates in the cylinder with a motion that approximates simple harmonic motion at $4200$ Revs per minute $\left(1 rev=1cycle\right).$ The mass of the piston is$0.24kg$ 

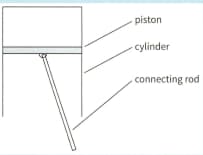
The amplitude of the oscillation is 12.5cm. Calculate: the maximum acceleration of the piston.

Shows the piston of a small car engine that oscillates in the cylinder with a motion that approximates simple harmonic motion at $4200$ revs per minute $\left(1rev=1cycle\right).$ The mass of the piston is $0.24kg$

Calculate the frequency of the oscillation.

This diagram shows the piston of a small car engine that oscillates in the cylinder with a motion that approximates simple harmonic motion at $4200$revs per minute $\left(1rev=1cycle\right).$. The mass of the piston is $0.24kg$

Explain what is meant by simple harmonic motion

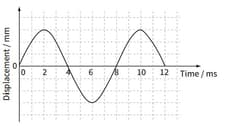
These graphs show the displacement of a body as it vibrates between two points.

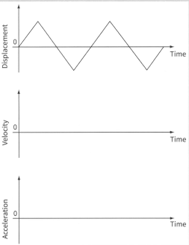
Make a copy of the three graphs

(i)On the second set of axes on your copy show the velocity of the body as it vibrates.
(ii)On the third set of axes on your copy, show the acceleration of the body.

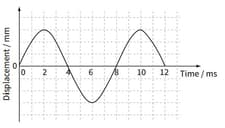
These graphs show the displacement of a body as it vibrates between two points

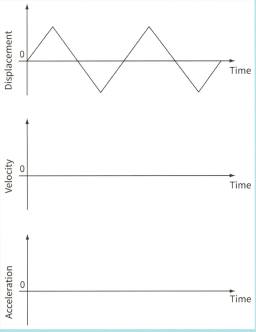
State and explain whether the body is moving with simple harmonic motion.

Use a copy of the graph and on the same axes sketch:

The acceleration of the particle

Use a copy of the graph and on the same axes sketch:

The velocity of the particle

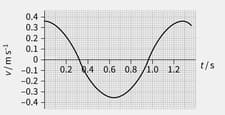
Figure shows how the velocity $v$ of a $2.0 \mathrm{kg}$ mass was found to vary with time $t$ during an investigation of the s.h.m. of a pendulum. Use the graph to estimate the following for the mass: The maximum restoring force that acted on it.

Figure shows how the velocity $v$ of a $2.0 \mathrm{kg}$ mass was found to vary with time $t$ during an investigation of the s.h.m. of a pendulum. Use the graph to estimate the following for the mass: Its maximum acceleration

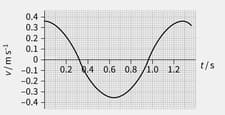
Figure shows how the velocity $v$ of a $2.0 \mathrm{kg}$ mass was found to vary with time $t$ during an investigation of the s.h.m. of a pendulum. Use the graph to estimate the following for the mass: Its maximum potential energy

Figure shows how the velocity $v$ of a $2.0 \mathrm{kg}$ mass was found to vary with time $t$ during an investigation of the s.h.m. of a pendulum. Use the graph to estimate the following for the mass: Its maximum velocity

A $50g$ mass is attached to a securely clamped spring. The mass is pulled downwards by $16mm$ and released, which causes it to oscillate with s.h.m. of time period of $0.84s$. Calculate the maximum velocity of the mass.

The pendulum of a clock is displaced by a distance of $4.0cm$ and it oscillates in s.h.m. with a period of $1.0s$. Calculate: its velocity when its displacement is $2.0cm$.

A trolley of mass $m$ Is fixed to the end of a spring. The spring can be compressed and extended. The spring has a force constant $k$. The other end of the spring is attached to a vertical wall. The trolley lies on a smooth horizontal table. The trolley oscillates when it is displaced from its equilibrium position. Show that the period $T$ Of the trolley is given by the equation: $T=2\pi \sqrt{\frac{m}{k}}$.