Equation of Waves

A traveling wave in a stretched string is described by the equation $y=A\sin \left(kx-\omega t\right)$. The maximum velocity of the particle is:

A simple harmonic wave-train is travelling in a gas in the positive direction of the $x$-axis. Its amplitude is $2 \mathrm{cm}$, velocity is $45 \mathrm{m} {\mathrm{s}}^{-1}$ and frequency is $75 \mathrm{Hz}$. Find out the displacement of the particle of the medium at a distance of $135 \mathrm{cm}$ from the origin in the direction of the wave at $t=3 \mathrm{s}$. Assume that the initial phase is zero.

A progressive wave has an amplitude $5 \mathrm{m}$ and wavelength $3 \mathrm{m}$. If the maximum average velocity of particle, in half time period, is $5 \mathrm{m} {\mathrm{s}}^{-1}$ and the wave is moving in the positive $x$-direction, then, which of the following may be the correct equation of the wave? (Here,$x$is in $\mathrm{meter}$)

A boat at anchor is rocked by waves whose successive crests are $100 \mathrm{m}$ apart and velocity is $25 \mathrm{m} {\mathrm{s}}^{-1}$. The boat bounces up once in every:

For a wave $y=y_0\sin (\omega t-kx)$, for what value of $\lambda$ is the maximum particle velocity equal to two times the wave velocity?

The linear density of a vibrating string is $1.3\times {10}^{-4}$ $\mathrm{kg} {\mathrm{m}}^{-1}$. A transverse wave is propagating on the string and is described by the equation $y = 0.021 \sin (x + 30t)$, where $x$and $y$ are measured in meter and $t$in second. The tension in the string is,

A man generates a symmetrical pulse in a string by moving his hand up and down. At $t=0$, the point in this hand moves downwards from mean position. The pulse travels with speed of $3 \mathrm{m} {\mathrm{s}}^{-1}$ on the string and his hand passes $6$ times in each second from the mean position. Then the point on the string at a distance $3 \mathrm{m}$ will reach its upper extreme first time at time $t$ equal to?

The equation of a wave is given by $y=10 \sin (\frac{2\pi t}{30}+\alpha )$. If the displacement is$5 \mathrm{cm}$ at $t=0$, then the total phase at $t=7.5 \mathrm{s}$ will be,

Equation of progressive wave is given by $y=a\mathrm{sin\pi }\left(\frac{t}{2}-\frac{x}{4}\right)$, where $t$ is in $\mathrm{second}$ and $x$ is in $\mathrm{metre}$. Then the distance through which the wave moves in $4 \mathrm{s}$ is

In a string, the speed of the wave is $10 \mathrm{m} {\mathrm{s}}^{-1}$ and its frequency is $100 \mathrm{Hz}$. The value of the phase difference at a distance $2.5 \mathrm{cm}$ will be

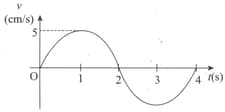
A certain transverse sinusoidal wave of wavelength $20 \mathrm{cm}$ is moving in the positive $x$ direction. The transverse velocity of the particle at $x=0$, as a function of time, is as shown. The amplitude of the motion is

Two particles of a medium, disturbed by the wave propagation, are at $x_1=0 \mathrm{cm}$ and $x_2=1 \mathrm{cm}$. The respective displacements (in $\mathrm{cm}$) of the particles can be given by the equations:
$y_1=2\sin 3\mathrm{\pi }t$ and $y_2=2\sin (3\mathrm{\pi }t-\frac{\mathrm{\pi }}{8})$.

In the above question, the displacement of particle, at$t = 1 \mathrm{s}$ and $x = 4 \mathrm{cm}$, is

Two particles of a medium, disturbed by the wave propagation, are at $x_1=0 \mathrm{cm}$ and $x_2=1 \mathrm{cm}$. The respective displacements (in $\mathrm{cm}$) of the particles can be given by the equations:
$y_1=2\sin 3\mathrm{\pi }t$ and $y_2=2\sin (3\mathrm{\pi }t-\frac{\mathrm{\pi }}{8})$.
The wave velocity is

Which of the following functions correctly represent the travelling wave equation for finite values of $x$ and $t$?