Standing Waves and Resonance

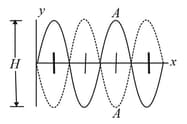
Two sinusoidal waves with the same amplitude and wavelength travel through each other along a string that is stretched along the $x$ axis. Their resultant wave is shown twice in the figure shown below, as the antinode $A$ travels from an extreme upward displacement to an extreme downward displacement in $6.0 \mathrm{ms}$. The tick marks along the axis are separated by $15 \mathrm{cm}$, height $H$ is $1.20 \mathrm{cm}.$ Let the equation for one of the two waves be of the form $y(x,t)=y_{\mathrm{m}}\sin (kx+\omega t).$ In the equation for the other wave, what are

(a) $y_m$

(b) $k$

(c) $\omega$

$\left(\mathrm{d}\right)$ the sign in front of $\mathrm{\omega }?$

A string oscillates according to the equation,
$y^{\text{'}}=\left(0.80 \mathrm{cm}\right)\sin \left[\left(\frac{\mathrm{\pi }}{3} {\mathrm{cm}}^{-1}\right)x\right]\cos \left[\left(40\mathrm{\pi } {\mathrm{s}}^{-1}\right)t\right]$
What is the

$\left(\mathrm{a}\right)$ amplitude

$\left(\mathrm{b}\right)$ speed of the two waves (identical except the direction of travel) whose superposition gives this oscillation?

$\left(\mathrm{c}\right)$ What is the distance between nodes?

$\left(\mathrm{d}\right)$ What is the transverse speed of a particle of the string at the position $x=2.1 \mathrm{cm}$ when $t=0.50 \mathrm{s}$?

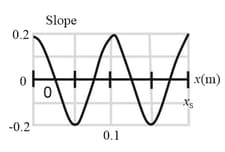
A sinusoidal wave travels along a string under tension. The figure shown below gives the slopes along the string at time $t=0.$ The scale of the $x$ axis is set by $x_{\mathrm{s}}=0.40 \mathrm{m}.$ What is the amplitude of the wave?

A transverse sinusoidal wave is moving along a string in the positive direction of $x$ axis with a speed of $70 \mathrm{m} {\mathrm{s}}^{-1}$. At $t=0,$ the string particle at $x=0$ has a transverse displacement of $4.0 \mathrm{cm}$ and is not moving. The maximum transverse speed of the string particle at $x=0 \text{is} 16 \mathrm{m} {\mathrm{s}}^{-1}$.

(a) What is the frequency of the wave?
(b) What is the wavelength of the wave?

If $y(x,t)=y_{\mathrm{m}}\sin (kx\pm \omega t+\varphi )$ is the form of the wave equation, what are

(c)$y_{\mathrm{m}}$

(d)$k$

(e)${\omega }_0$

(f)$\varphi$

$\left(\mathrm{g}\right)$ the correct choice of sign in front of $\omega ?$

Use the wave equation to find the speed of a wave given in terms of the general function $h(x, t)$
$y(x,t)=(4.00 \mathrm{mm})\sin \left[\left(22.0 {\mathrm{m}}^{-1}\right)x+\left(8.00 {\mathrm{s}}^{-1}\right)t\right]$.

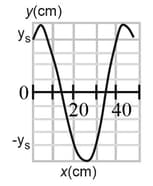
A sinusoidal transverse wave is traveling along a string in the negative direction of an $\mathrm{x}$ axis. In the Figure shown below shows a plot of the displacement as a function of position at time $\mathrm{t}=0$, the scale of the $\mathrm{y}$ axis is set by ${\mathrm{y}}_{\mathrm{s}}=4.0 \mathrm{cm}$. The string tension is $3.6 \mathrm{N}$, and its linear density is $28 \mathrm{g} {\mathrm{m}}^{-1}$. Find the
(a) amplitude.
(b) wavelength,
(c) wave speed, and (d) period of the wave.
(e) Find the maximum transverse speed of a particle in the string. 

If the wave is of the form $y(x, t)=y_{\mathrm{m}}\sin (kx\pm \omega t+\varphi ),$ what are

(f) $k$,

(g) $\omega$,
(h) $\mathrm{\varphi }$ and
(i) the correct choice of sign in front of $\mathrm{\omega }?$

The speed of a transverse wave on a string is $115 \mathrm{m} {\mathrm{s}}^{-1}$ when the string tension is $200 \mathrm{N}$. To what value must the tension be changed to raise the wave speed to $223 \mathrm{m} {\mathrm{s}}^{-1}?$

A uniform rope of mass $m$ and length $L$ hangs from a ceiling.
(a) Show that the speed of a transverse wave on the rope is a function of $y$, the distance from the lower end, and is given by $v=\sqrt{gy}$
(b) Show that the time a transverse wave takes to travel the length of the rope is given by $t=2\sqrt{\frac{L}{g}}$

A string along which waves can travel is $2.70 \mathrm{m}$ long and has a mass of $130 \mathrm{g}$. The tension in the string is $36.0 \mathrm{N}$ . What must be the frequency of traveling waves of amplitude $7.70 \mathrm{mm}$ for the average power to be $170 \mathrm{W}?$

If a wave $y(x,t)=(5.0 \mathrm{mm})\sin (kx+(600 \mathrm{rad} {\mathrm{s}}^{-1})t+\varphi )$ travels along a string, how much time does any given point on the string take to move between displacements $y=+2.0 \mathrm{mm}$ and $y=-2.0 \mathrm{mm}?$

Four waves are to be sent along the same string, in the same direction:
$\begin{array}{l}{y}_1(x,t)=(5.00 \mathrm{mm})\sin (4\pi x-400\pi t)\\ y_2(x,t)=(5.00 \mathrm{mm})\sin (4\pi x-400\pi t+0.8\pi )\\ y_3(x,t)=(5.00 \mathrm{mm})\sin (4\pi x-400\pi t+\pi )\\ y_4(x,t)=(5.00 \mathrm{mm})\sin (4\pi x-400\pi t+1.8\pi )\end{array}$
What is the amplitude of the resultant wave?

The following two waves are sent in opposite directions on a horizontal string to create a standing wave in a vertical plane:
$\begin{array}{l}{y}_1(x,t)=(6.00 \mathrm{mm})\sin (12.0\pi \mathrm{x}-300\pi t)\\ y_2(x,t)=(6.00 \mathrm{mm})\sin (12.0\pi \mathrm{x}+300\pi t)\end{array}$
with $x$ in meters and $t$ in seconds. An antinode is located at point $\mathrm{A}$. In the time interval that point takes to move from maximum upward displacement to maximum downward displacement, how far does each wave move along the string?

A sinusoidal wave is travelling on a string with speed $40 \mathrm{cm} {\mathrm{s}}^{-1}$. The displacement of the particles of the string at $\mathrm{x}=10 \mathrm{cm}$ varies with time according to $y=(4.0 \mathrm{cm})sin\left[5.0-\left(4.0 {\mathrm{s}}^{-1}\right)t\right].$ The linear density of the string is $4.0 \mathrm{g} {\mathrm{cm}}^{-1}.$ What are
(a) the frequency
(b) the wavelength of the wave?

If the wave equation is of the form $y(x,t)=y_{\mathrm{m}}sin(kx\pm \omega t),$ what are
(c) $y_{\mathrm{m}},\left(d\right)k,\left(e\right)\omega ,$
(f) the correct choice of sign in front of $\omega$
(g) What is the tension in the string?

Two sinusoidal waves of the same period, with amplitudes of $5.0$ and $7.0 \mathrm{mm}$, travel in the same direction along a stretched string. They produce a resultant wave with an amplitude of $10.0 \mathrm{mm}$. The phase constant of the $5.0 \mathrm{mm}$ wave is $0$. What is the phase constant of the $7.0 \mathrm{mm}$ wave?

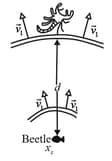
A sand scorpion can detect the motion of a nearby beetle (its prey) by the waves the motion sends along the sand surface (in the figure shown below). The waves are of two types, transverse waves travelling at $v_{\mathrm{t}}=50 \mathrm{m} {\mathrm{s}}^{-1}$ and longitudinal waves traveling at $v_{\mathrm{l}}=150 \mathrm{m} {\mathrm{s}}^{-1}$. If a sudden motion sends out such waves, a scorpion can tell the distance of the beetle from the difference $∆t$ in the arrival times of the waves at its leg nearest the beetle. What is the time difference if the distance to the beetle is $37.5 \mathrm{cm}?$

What are

(a) the lowest frequency

(b) the second lowest frequency

(c) the third lowest frequency

for standing waves on a wire that is $10.0 \mathrm{m}$ long, has a mass of $100 \mathrm{g}$, and is stretched under a tension of $275 \mathrm{N}$?

The function, $y(x, t)=(15.0 \mathrm{cm})\cos (\mathrm{\pi }x-15\text{π}t)$, with $x$ in $\mathrm{meters}$ and $t$ in $\mathrm{seconds}$, describes a wave on a taut string. What is the transverse speed for a point on the string at an instant when that point has the displacement $y=+6.00 \mathrm{cm}$?

What is the speed of a transverse wave in a rope of length $1.75 \mathrm{m}$ and mass $60.0 \mathrm{g}$ under a tension of $500 \mathrm{N}$?

The equation of a transverse wave travelling along a very long string is $y=3.0sin(0.020\pi x-4.0\pi t),$ where $x$ and $y$ are expressed in centimetres, and $t$ is in seconds. Determine

(a) the amplitude

(b) the wavelength

(c) the frequency

(d) the speed

(e) the direction of propagation of the wave

(f) the maximum transverse speed of a particle in the string.

(g) What is the transverse displacement at $x=3.5 \mathrm{cm}$ when $t=0.26 \mathrm{s}?$

A sinusoidal wave is sent along a string with a linear density of $\mu =5.0 \mathrm{g} {\mathrm{m}}^{-1}$. As it travels, the kinetic energies of the mass elements along the string vary. The figure shown below gives the rate $\frac{\mathrm{dK}}{dt}$ at which kinetic energy passes through the string elements at a particular instant, plotted as a function of distance $x$ along the string. The figure shown below is similar except that it gives the rate at which kinetic energy passes through a particular mass element (at a particular location), plotted as a function of time $\mathrm{t}$. For both figures, the scale on the vertical (rate) axis is set by $R_{\mathrm{s}}=10 \mathrm{W}$. What is the amplitude of the wave?