R Chandra Solutions for Chapter: Heron's Formula, Exercise 1: TEST YOUR SKILLS

Find the area of a triangular park whose sides are $40 \mathrm{m}, 32 \mathrm{m}$ and $24\mathrm{}\mathrm{m}$.

Find the area of an isosceles triangle, the ratio of whose equal side to its base is $3:2$ and the perimeter is $32 \mathrm{c}\mathrm{m}$.

A triangular park has sides $120 \mathrm{m}$, $80 \mathrm{m}$ and $50 \mathrm{m}$. A gardener has to put a fence all around it and also plant grass inside. How much area does he need to plant? Find the cost of fencing it with barbed wire at the rate of $\mathrm{₹}$ $20$ per meter, leaving $3 \mathrm{m}$ wide space for a gate on one side.

The sides of a triangular plot are in the ratio of $6:7:8$ and its perimeter is $420 \mathrm{m}$. Find its area.

 A farmer has a triangular field with sides $240 \mathrm{m}$, $200 \mathrm{m}$ and $360 \mathrm{m}$, where he grew wheat. In another triangular field with sides $240 \mathrm{m}$, $320 \mathrm{m}$ and $400 \mathrm{m}$ adjacent to the previous field, he wanted to grow potatoes and onions (see figure). He divided the field into two parts by joining the mid-point of the longest side to the opposite vertex and grew potatoes in one part and onions in the other part. How much area (in hectares) has been used for wheat, potatoes and onions?

Note: $\mathrm{10,000} {\mathrm{m}}^2=1 \mathrm{h}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{e}$

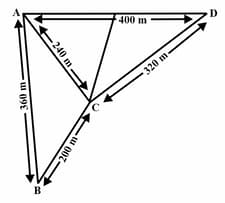
Students of a school staged a rally for cleanliness campaign. They walked through the lanes in two groups. One group walked through the lanes $\mathrm{A}\mathrm{B}$, $\mathrm{B}\mathrm{C}$ and $\mathrm{C}\mathrm{A}$; while the other through $\mathrm{A}\mathrm{C}$, $\mathrm{C}\mathrm{D}$ and $\mathrm{D}\mathrm{A}$ (see figure). Then they cleaned the area enclosed within their lanes. If $\mathrm{A}\mathrm{B}=9 \mathrm{m}$, $\mathrm{B}\mathrm{C}=40 \mathrm{m}$, $\mathrm{C}\mathrm{D}=15 \mathrm{m}$, $\mathrm{D}\mathrm{A}=28 \mathrm{m}$ and $\mathrm{\angle }\mathrm{B}=90°$, Which group cleaned more area and by how much? Find the total area cleaned by the students (neglecting the width of the lanes).
 

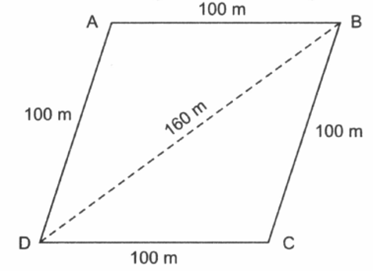
Parul has a piece of land which is in the shape of a rhombus (see fig.). She wants her daughter and son to work on the land and produce different crops. She divided the land in two equal parts. If the perimeter of the land is $400 \mathrm{m}$ and one of the diagonal is $160 \mathrm{m}$, how much area each of them will get for their crops?

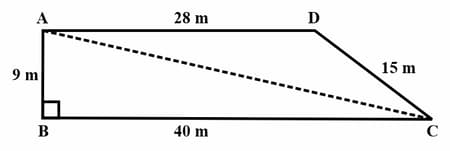
Find the height of a trapezium in which parallel sides are $25 \mathrm{c}\mathrm{m}$ and $77 \mathrm{c}\mathrm{m}$ and non-parallel sides and $26 \mathrm{c}\mathrm{m}$ and $60 \mathrm{c}\mathrm{m}$. Given the area of the trapezium as $1644 \mathrm{c}{\mathrm{m}}^2$.