R K Bansal Solutions for Exercise 1: EXERCISE

A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole the angle of elevation of the top of the tower is $60°$ and the angle of depression of the bottom of the tower is $30°$. Find The height of the pole, if the height of the tower is $75\mathrm{m}$.

From a point, $36\mathrm{m}$ above the surface of a lake, the angle of elevation of a bird is observed to be $30°$ and angle of depression of its image in the water of the lake is observed to be $60°$. Find the actual height of the bird above the surface of the lake. 

A man observes the angle of elevation of the top of a building to be $30°$. He walks towards it in a horizontal line through its base. On covering $60\mathrm{m}$, the angle of elevation changes to $60°$. Find the height of the building correct to the nearest metre.

As observed from the top of a $80 \mathrm{m}$ tall lighthouse, the angles of depression of two ships, on the same side of the lighthouse in horizontal line with its base, are $30°$ and $40°$ respectively. Find the distance between the two ships. Give your answer correct to the nearest meter.

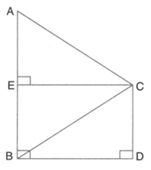
In the given figure, from the top of a building $\mathrm{AB}=60\mathrm{m}$ high, the angles of depression of the top and bottom of a vertical lamp post $\mathrm{CD}$ are observed to be $30°$ and $60°$ respectively. Find the horizontal distance between $\mathrm{AB}$ and $\mathrm{CD}$

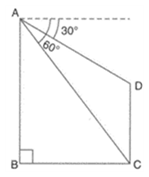
In the given figure, from the top of a building $\mathrm{AB}=60\mathrm{m}$ high, the angles of depression of the top and bottom of a vertical lamp post $\mathrm{CD}$ are observed to be $30°$ and $60°$ respectively. Find the height of the lamp post.

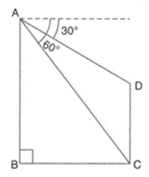
An aeroplane, at an altitude of $250\mathrm{m}$ observes the angles of depression of two boats on the opposite banks of a river to be $45°$ and $60°$ respectively. Find the width of the river. Write the answer correct to the nearest whole number.

The horizontal distance between two towers is $120\mathrm{m}$. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the top of the second tower is $30°$ and $24°$ respectively. Find the height of the two towers with approximate value and find difference between them.