R. D. Sharma Solutions for Chapter: Areas Related to Circles, Exercise 3: EXERCISE 13.3

A chord of a circle of radius $14 \mathrm{cm}$ makes a right angle at the centre. Find the areas of the minor and major segments of the circle.

A chord $10 \mathrm{cm}$ long is drawn in a circle whose radius is $5\sqrt{2} \mathrm{cm}$. Find area of both the segments.

A chord $AB$ of a circle, of radius $14 \mathrm{cm}$ makes an angle of $60°$ at the center of the circle. Find the area of the minor segment of the circle. (Use $\pi = 22/7$).

Find the area of minor segment of a circle of radius $14 \mathrm{cm}$, when the angle of the corresponding sector is $60°$.

A chord of a circle of radius$20 \mathrm{cm}$sub tends an angle of $90°$at the center. Find the area of the corresponding major segment of the circle (Use $\pi =3.14$).

The radius of a circle with centre $\mathrm{O}$ is $5 \mathrm{cm}$. Two radii $\mathrm{OA}$ and $\mathrm{OB}$ are drawn at right angles to each other. Find the areas of the segments made by the chord $\mathrm{AB}$. $(\mathrm{\pi }=3.14)$. If the area of the minor segment is $\mathrm{p} {\mathrm{cm}}^2$, then find the value of $\mathrm{p}$.

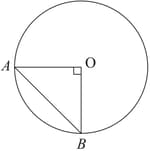
$AB$ is the diameter of a circle, centre $O, C$ is a point on the circumference such that $\angle COB=\theta$. The area of the minor segment cut off by $AC$ is equal to twice the area of the sector $BOC$. Prove that  $\sin \frac{\theta }{2}\cos \frac{\theta }{2}$$=\pi$ $\left(\frac{1}{2}-\frac{\theta }{120}\right)$.

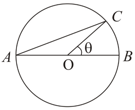
A chord of a circle subtends an angle of $\theta$ at the centre of the circle. The area of the minor segment cut off by the chord is one eighth of the area of the circle. Prove that $8$ $\sin \frac{\theta }{2}\cos \frac{\theta }{2}+\pi =\frac{\pi \theta }{45°}$.