Resnick & Halliday Solutions for Chapter: Capacitance, Exercise 1: Problems

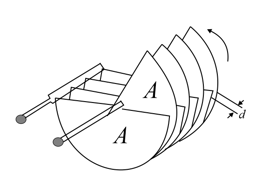
Figure shows a variable "air gap" capacitor for manual tuning. Alternate plates are connected together; one group of plates is fixed in position, and the other group is capable of rotation. Consider a capacitor of $n=8$ plates of alternating polarity, each plate having area $A=1.50{\mathrm{cm}}^2$ and separated from adjacent plates by distance $d=3.40\mathrm{mm}$. What is the maximum capacitance of the device?

The space between the two concentric conducting spherical shells of radii $b=1.70 \mathrm{cm}$ and $a=1.20 \mathrm{cm}$ is filled with a substance of dielectric constant $\kappa =6.91.$ A potential difference $V=73.0 \mathrm{V}$ is applied across the inner and outer shells. Determine (a) the capacitance of the device, (b) the free charge $q$ on the inner shell and (c) the charge $q^{\text{'}}$ induced along the surface of the inner shell.

You have two flat metal plates, each of area $1.00 {\mathrm{m}}^2,$ with which you have to construct a parallel-plate capacitor. (a) If the capacitance of the device is to be $2.00 \mathrm{F}$ , what must be the separation between the plates? (b) Could this capacitor actually be constructed?

The two metal objects shown below have $+70 \mathrm{pC}$ and $-70 \mathrm{pC}$ charges and results in a $35 \mathrm{V}$ potential difference between them. (a) What is the capacitance of the system? (b) If the charges are changed to$+200 \mathrm{pC}$ and $-200 \mathrm{pC}$, what will happen to the capacitance? (c) What will happen to the potential difference?

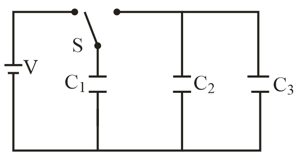
In the Figure,$V=12 \mathrm{V}, C_1=10 \mathrm{\mu F}$ and $C_2=C_3=20 \mathrm{\mu F}$. Switch $\mathrm{S}$ is first thrown to the left side until capacitor $1$ reaches equilibrium. Then the switch is thrown to the right. When equilibrium is reached again, how much charge is on capacitor $1 ?$

A $100 \mathrm{pF}$ capacitor is charged to a potential difference of $80.0 \mathrm{V},$  after which the charging battery is disconnected. The capacitor is then connected in parallel with a second (initially uncharged) capacitor. If the potential difference across the first capacitor drops to $35.0 \mathrm{V},$  what is the capacitance of this second capacitor?

The plates of a spherical capacitor have radii $37.0 \mathrm{mm}$ and $40.0 \mathrm{mm}.$ (a) Calculate the capacitance. (b) What must be the plate area of a parallel-plate capacitor with the same plate separation and capacitance?

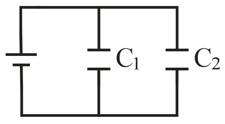
In figure two parallel-plate capacitors (with air between the plates) are connected to a battery. Capacitor $1$ has a a plate area of $1.5 {\mathrm{cm}}^2$ and an electric field (between its plates) of magnitude $3500 \mathrm{V} {\mathrm{m}}^{-1}.$ Capacitor $2$ has a plate area of $0.70 {\mathrm{cm}}^2$ and an electric field of magnitude$1500 \mathrm{V} {\mathrm{m}}^{-1}$. (a) What is the total charge on the two capacitors? (b) If the first plate area is cut in half, does the total charge increase, decrease, or remain the same?