Resnick & Halliday Solutions for Chapter: Electric Potential, Exercise 1: Problems

In the figure, a plastic rod which has a uniformly distributed charge $Q=-28.9 \mathrm{pC}$ has been bent into a circular arc of a radius $R=3.71 \mathrm{cm}$ and the central angle $\text{ϕ}=120°$. With $V=0$ at infinity, what is the electric potential at $P$, the centre of curvature of the rod?

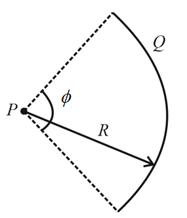
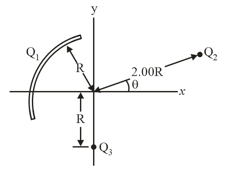
In the given figure, what is the net electric potential at the origin due to the circular arc of charge $Q_1=+7.21 \mathrm{pC}$, the two particles of charges $Q_2=4.00Q_1$ and $Q_3=-2.00Q_1$? The arc's centre of curvature is at the origin and its radius is $R=2.00 \mathrm{m}$, the angle indicated is $\text{θ}=35.0°$. What is the net electric potential at the origin if both $Q_1$ and $R$ are doubled?

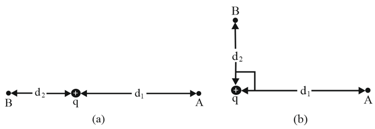
Consider a particle with charge $q=3.0 \mathrm{nC}$, point $A$ at distance $d_1=2.0 \mathrm{m}$ from $q$ and the point $B$ at distance $d_2=1.0 \mathrm{m}$. If $A$ and $B$ are diametrically opposite to each other as in the figure, (a) what is the electric potential difference $V_{\mathrm{A}}-V_{\mathrm{B}}$? (b) what is the electric potential difference if $A$ and $B$ are located as in the figure (b)?

The electric potential at points in an $xy$ plane is given by, $V=\left(2.00 \mathrm{V} {\mathrm{m}}^{-2}\right)x^2-\left(3.00 \mathrm{V} {\mathrm{m}}^{-2}\right)y^2$. What are,

(a) the magnitude and (b) the angle (relative to $+x$) of the electric field at the point $(4.00 \mathrm{m}\text{,} 2.00 \mathrm{m})$?

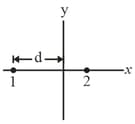
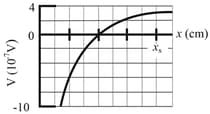
Two charged particles are shown in figure. (a) Particle $1$, with charge $q_1$, is fixed in place at distance $d$. Particle $2$, with charge $q_2$, can be moved along the $x$-axis. Figure (b) gives the net electric potential $V$ at the origin due to the two particles as a function of the $x$-co-ordinate of particle $2$. The scale of the $x$-axis is set by, $x_{\mathrm{s}}=16.0 \mathrm{cm}$. The plot has an asymptote of $V=5.92\times {10}^{-7} \mathrm{V}$ as $x\to \infty$. What is $q_2$ in terms of $e$?

                 $\left(\mathrm{a}\right) \left(\mathrm{b}\right)$                              

An infinite non-conducting sheet has a surface charge density, $\text{σ}=+5.80 \mathrm{pC} {\mathrm{m}}^2$.

(a) How much work is done by the electric field due to the sheet if a particle of charge, $q=+1.60\times {10}^{-19} \mathrm{C}$ is moved from the sheet to a point $P$ at distance, $d=6.15 \mathrm{cm}$ from the sheet?

(b) If the electric potential $V$ is defined to be $-5.00 \mathrm{mV}$ on the sheet, what is $V$ at $P$?

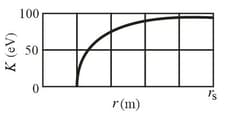
Figure (a) shows an electron moving along the electric dipole axis towards the negative side of the dipole. The dipole is fixed in place. The electron was initially very far from the dipole with kinetic energy $300 \mathrm{eV}$. Figure (b) gives the kinetic energy $K$ of the electron versus its distance $r$ from the dipole centre. The scale of the horizontal axis is set by, $r_{\mathrm{s}}=0.20 \mathrm{m}$. What is the magnitude of the dipole moment?

 $\left(\mathrm{a}\right) \left(\mathrm{b}\right)$

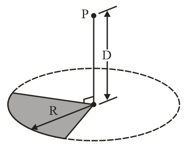
A plastic disk of radius, $R=64.0\mathrm{cm}$ is charged on one side with a uniform surface charge density $\sigma =7.73f \mathrm{C} {\mathrm{m}}^{-2}$ , and then three quadrants of the disk are removed. The remaining quadrant is shown in the figure with $V=0$ at infinity, what is the potential due to the remaining quadrant at point $P$, which is on the central axis of the original disk at distance $D=45.0\mathrm{cm}$ from the original centre?