Resnick & Halliday Solutions for Chapter: Gauss' Law, Exercise 1: Problems
Resnick & Halliday Physics Solutions for Exercise - Resnick & Halliday Solutions for Chapter: Gauss' Law, Exercise 1: Problems
Attempt the practice questions on Chapter 23: Gauss' Law, Exercise 1: Problems with hints and solutions to strengthen your understanding. Principles Of Physics International Student Version solutions are prepared by Experienced Embibe Experts.
Questions from Resnick & Halliday Solutions for Chapter: Gauss' Law, Exercise 1: Problems with Hints & Solutions
The figure shows two nonconducting spherical shells fixed in place. Shell has uniform surface charge density on its outer surface and radius ; shell has uniform surface charge density on its outer surface and radius the shell centers are separated by In unit-vector notation, what is the net electric field at
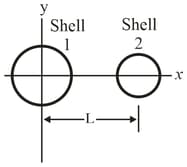
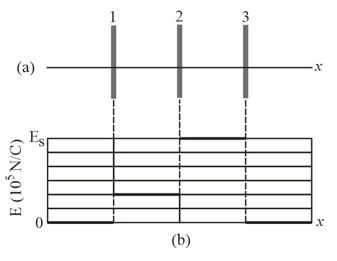
Figure shows three plastic sheets that are large, parallel, and uniformly charged. Figure gives the component of the net electric field along the -axis through the sheets. The scale of the vertical axis is set by What is the ratio of the charge density on sheet to that on sheet ?
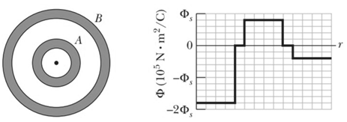
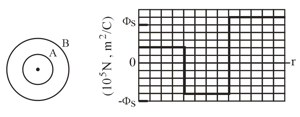
Flux and conducting shells. A charged particle is held at the center of two concentric conducting spherical shells. Figure shows a cross section. Figure gives the net flux through a Gaussian sphere centered on the particle, as a function of the radius of the sphere. The scale of the vertical axis is set by . What are the charge of the central particle and the net charges of shell and shell ?
(a) (b)
Space vehicles traveling through Earth's radiation belts can intercept a significant number of electrons. The resulting charge buildup can damage electronic components and disrupt operations. Suppose a spherical metal satellite in diameter accumulates of charge in one orbital revolution. Find the resulting surface charge density. Calculate the magnitude of the electric field just outside the surface of the satellite, due to the surface charge.
When a shower is turned on in a closed bathroom, the splashing of the water on the bare tub can fill the room's air with negatively charged ions and produce an electric field in the air as great as Consider a bathroom with dimensions Along with the ceiling, floor, and four walls, approximate the electric field in the air as being directed perpendicular to the surface and as having a uniform magnitude of . Also, treat those surfaces as forming a closed Gaussian surface around the room's air. What are (a) the volume charge density and (b) the number of excess elementary charges per cubic meter in the room's air?
A square metal plate of edge length and negligible thickness has a total charge of . (a) Estimate the magnitude of the electric field just off the center of the plate (at a distance of from the center) by assuming that the charge is spread uniformly over the two faces of the plate. (b) Estimate at a distance of (larger relative to the plate size) by assuming that the plate is a charged particle.
A charged particle is suspended at the center of two concentric spherical shells that are very thin and made of nonconducting material. Figure (a) shows a cross-section. Figure (b) gives the net flux through a Gaussian sphere centered on the particle, as a function of the radius of the sphere. The scale of the vertical axis is set by (a) What is the charge of the central particle? What are the net charges of (b) shell and (c) shell
(a) (b)
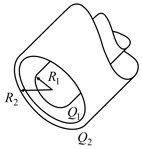
The figure given below is a section of a conducting rod of radius and length inside a thin-walled coaxial conducting cylindrical shell of radius and the (same) length The net charge on the rod is that on the shell is . What are the (a) magnitude and (b) direction (radially inwards or outwards) of the electric field at radial distance What are (c) and (d) the direction at What is the charge on the (e) interior and (f) exterior surface of the shell?