Resnick & Halliday Solutions for Chapter: Magnetic Fields, Exercise 1: Problems
Resnick & Halliday Physics Solutions for Exercise - Resnick & Halliday Solutions for Chapter: Magnetic Fields, Exercise 1: Problems
Attempt the practice questions on Chapter 28: Magnetic Fields, Exercise 1: Problems with hints and solutions to strengthen your understanding. Principles Of Physics International Student Version solutions are prepared by Experienced Embibe Experts.
Questions from Resnick & Halliday Solutions for Chapter: Magnetic Fields, Exercise 1: Problems with Hints & Solutions
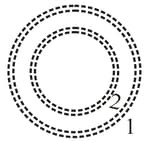
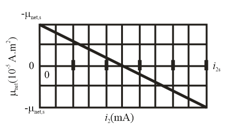
In figure (a), two concentric coils, lying in the same plane, carry currents in opposite directions. The current in the larger coil is fixed. Current in coil can be varied. Figure (b) gives the net magnetic moment of the two-coil system as a function of . The vertical axis scale is set by, and the horizontal axis scale is set by, . If the current in coil is then reversed, what is the magnitude of the net magnetic moment of the two-coil system when
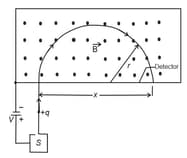
A mass spectrometer (fig.) is used to separate uranium ions of mass and charge from related species. The ions are accelerated through a potential difference of and then pass into a uniform magnetic field, where they are bent in a path of radius . After traveling through and passing through a slit of width and height they are collected in a cup. (a) What is the magnitude of the (perpendicular) magnetic field in the separator? If the machine is used to separate out of material per hour, calculate (b) the current of the desired ions in the machine and (c) the thermal energy produced in the cup in .
An electric field of and a perpendicular magnetic field of act on a moving electron to produce no net force. What is the electron's speed?
An ion source is producing ions, which have charge and mass The ions are accelerated by a potential difference of and pass horizontally into a region in which there is a uniform vertical magnetic field of magnitude . Calculate the strength of the electric field, to be set up over the same region, that will allow the ions to pass through without any deflection.
In a nuclear experiment a proton with kinetic energy moves in a circular path in a uniform magnetic field. What energy must (a) an alpha particle and (b) a deuteron have if they have to circulate in the same circular path?
An electron that has an instantaneous velocity of is moving through the uniform magnetic field . (a) Find the force in newton on the electron due to the magnetic field. (b) Repeat your calculation for a proton having the same velocity.
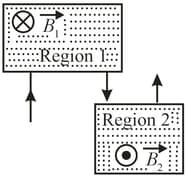
In the figure shown, an electron with an initial kinetic energy of enters region 1 at time That region contains a uniform magnetic field directed into the page with magnitude . The electron goes through a half-circle exits region 1, and then heads towards region 2 across a gap of There is an electric potential difference of across the gap, with a polarity such that the electron's speed increases uniformly as it traverses the gap. Region 2 contains a uniform magnetic field directed out of the page, with magnitude . The electron goes through a half-circle and then leaves region 2. At what time does it leave?
An alpha particle can be produced in certain radioactive decays of nuclei and consists of two protons and two neutrons. The particle has a charge of and a mass where is the atomic mass unit, with Suppose an alpha particle travels in a circular path of radius in a uniform magnetic field with . Calculate
(a) its speed,
(b) its period of revolution,
(c) its kinetic energy, and
(d) the potential difference through which it would have to be accelerated to achieve this energy.
(e) If the field magnitude is doubled, what is the ratio of the new value of kinetic energy to the initial value?