Resnick & Halliday Solutions for Chapter: Rotation, Exercise 1: Problems

A thin rod of length $0.75 \mathrm{m}$ and mass $0.42 \mathrm{kg}$ is suspended freely from one end. It is pulled to one side and then allowed to swing like a pendulum, passing through its lowest position with angular speed $3.5 \mathrm{rad} {\mathrm{s}}^{-1}$. Neglecting friction and air resistance, find (a) the rod's kinetic energy at its lowest position and (b) how far above that position the center of mass rises.

Disks $A$ and $B$ each have a rotational inertia of  $0.300 \mathrm{kg} {\mathrm{m}}^2$ about the central axis and a radius of $20.0 \mathrm{cm}$ and are free to rotate on a central rod through both of them. To set them spinning around the rod in the same direction, each is wrapped with a string that is then pulled for $10.0 \mathrm{s}$ (the string detaches at the end). The magnitudes of the forces pulling the strings are $30.0 \mathrm{N}$ for disk $A$ and $20.0 \mathrm{N}$ for disk $B$. After the strings detach, the disks happen to collide and the frictional force between them brings them to the same final angular speed in $6.00 \mathrm{s}$. What is
(a) the magnitude of the average frictional torque that brings them to the final angular speed and (b) the loss in kinetic energy as that torque acts on them?
(c) Where did the "lost energy" go?

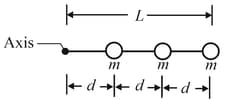
In the figure shown below, three $0.0100 \mathrm{kg}$ particles have been glued to a rod of length $L=6.00 \mathrm{cm}$ and negligible mass and can rotate around a perpendicular axis through point $O$ at one end. How much work is required to change the rotational rate

(a) from $0$ to$20.0 \mathrm{rad} {\mathrm{s}}^{-1}$,

(b) from $20.0 \mathrm{rad} {\mathrm{s}}^{-1}$ to $40.0 \mathrm{rad} {\mathrm{s}}^{-1}$ and

(c) from$40.0 \mathrm{rad} {\mathrm{s}}^{-1}$ to $60.0 \mathrm{rad} {\mathrm{s}}^{-1}$?

(d) What is the slope of a plot of the assembly's kinetic energy (in joules) versus the square of its rotation rate (in radians squared per second-squared)?

A meter stick is held vertically with one end on the floor and is then allowed to fall. Find the speed of the other end just before it hits the floor, assuming that the end on the floor does not slip. (Hint: Consider the stick to be a thin rod and use the conservation of energy principle).

A uniform cylinder of radius$12 \mathrm{cm}$ and mass $25 \mathrm{kg}$ is mounted to rotate freely about a horizontal axis that is parallel to and $5.0 \mathrm{cm}$ from the central longitudinal axis of the cylinder.
(a) What is the rotational inertia of the cylinder about the axis of rotation? (b) If the cylinder is released from rest with its central longitudinal axis at the same height as the axis about which the cylinder rotates, what is the angular speed of the cylinder as it passes through its lowest position?

A tall, cylindrical chimney falls over when its base is ruptured. Treat the chimney as a thin rod of length $55.0 \mathrm{m}$. At the instant it makes an angle of $35.0°$ with the vertical as it falls, what are (a) the radial acceleration of the top. and (b) the tangential acceleration of the top. (Hint : Use energy considerations, not a torque.)
(c) At what angle $\mathrm{\theta }$ is the tangential acceleration equal to $g$?

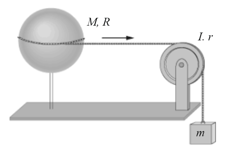
A uniform spherical shell of mass $M=4.5 \mathrm{kg}$ and radius $R=8.5 \mathrm{cm}$ can rotate about a vertical axis on frictionless bearings (In the figure shown below). A massless cord passes around the equator of the shell, over a pulley of rotational inertia $I=3.0\times {10}^{-3} \mathrm{kg}·{\mathrm{m}}^2$ and radius $r=5.0 \mathrm{cm}$, and is attached to a small object of mass $m=0.60 \mathrm{kg}$. There is no friction on the pulley's axle; the cord does not slip on the pulley. What is the speed of the object when it has fallen $82 \mathrm{cm}$ after being released from rest? Use energy considerations.

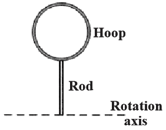
In the figure shown below a rigid assembly of a thin hoop (of mass $m$ and radius $R=0.150 \mathrm{m}$) and a thin radial rod (of mass $m$ and length $L=2.00 R$). The assembly is upright, but if we give it a slight nudge, it will rotate around a horizontal axis in the plane of the rod and hoop, through the lower end of the rod. Assuming that the energy given to the assembly in such a nudge is negligible, what would be the assembly's angular speed about the rotation axis when it passes through the upside-down (inverted) orientation?