Rose Harrison and Clara Huizink Solutions for Exercise 18: Practice 6

When you ride a Ferris wheel, your vertical height above the ground changes. The relationship between your height above the ground and the time for a complete revolution of the wheel can be modelled with a sinusoidal graph like this:

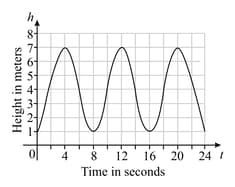
Determine your height above the ground after $8$ seconds.

When you ride a Ferris wheel, your vertical height above the ground changes. The relationship between your height above the ground and the time for a complete revolution of the wheel can be modelled with a sinusoidal graph like this:

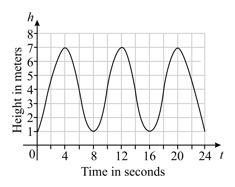
Determine how long it takes for one complete revolution of the wheel.

When you ride a Ferris wheel, your vertical height above the ground changes. The relationship between your height above the ground and the time for a complete revolution of the wheel can be modelled with a sinusoidal graph like this:

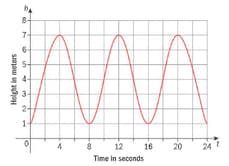
The Ferris wheel is circular. Its radius  is $a m$, find the value of $a.$

When you ride a Ferris wheel, your vertical height above the ground changes. The relationship between your height above the ground and the time for a complete revolution of the wheel can be modelled with a sinusoidal graph like this:

Find a function that models this graph.

The height in meters of the tide above the mean sea level one day at Bal Harbor can be modelled by the function $\mathrm{h}\left(\mathrm{t}\right)=3\sin (30°\mathrm{t})$, where $\mathrm{t}$ is the number of hours after midnight.

Find $\mathrm{h}$ when $\mathrm{t}=0,6,12,18$ and $24$ hours.

The height in meters of the tide above the mean sea level one day at Bal Harbor can be modelled by the function $h\left(t\right)=3\sin (30°t)$, where $t$ is the number of hours after midnight. The height of the tide at $4 o\text{'}$ clock in the afternoon is $a m$. Find the value of $a$.

The height in meters of the tide above the mean sea level one day at Bal Harbor can be modelled by the function $h\left(t\right)=3\sin (30°t)$, where $t$ is the number of hours after midnight.

A ship can cross the harbour if the tide is at least $2m$ above the average sea level. Determine the times when it can cross the harbour.

One day, high tide in Venice, Italy was at midnight. The water level at high tide was $3.3m$, and later at low tide the water level was $0.1m$. Assume that the next high tide is $12$ hours later and that the height of the water level can be modelled with a sinusoidal function.

Draw a graph of your function.