Rose Harrison, Clara Huizink, Aidan Sproat Clements and, Marlene Torres Skoumal Solutions for Exercise 10: Practice 2
Rose Harrison Mathematics Solutions for Exercise - Rose Harrison, Clara Huizink, Aidan Sproat Clements and, Marlene Torres Skoumal Solutions for Exercise 10: Practice 2
Attempt the free practice questions from Exercise 10: Practice 2 with hints and solutions to strengthen your understanding. Extended MYP Mathematics A Concept based approach Years 4 & 5 solutions are prepared by Experienced Embibe Experts.
Questions from Rose Harrison, Clara Huizink, Aidan Sproat Clements and, Marlene Torres Skoumal Solutions for Exercise 10: Practice 2 with Hints & Solutions
A school bus needs to travel at least once down every road of a housing estate. The bus enters and leaves the estate at on the map below, where the weights represent the lengths of the roads in meters.
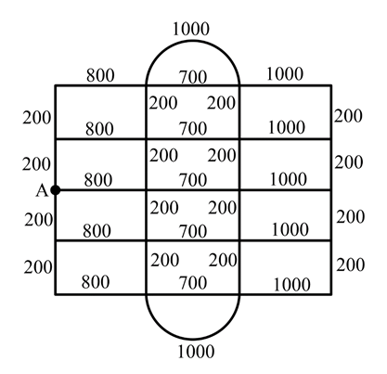
Determine the total weight of the network.
A school bus needs to travel at least once down every road of a housing estate. The bus enters and leaves the estate at on the map below, where the weights represent the lengths of the roads in meters.

Determine the total weight of the network.
By considering the network's odd vertices, determine the minimum distance that the bus must travel if it is to journey down every road on the estate.
A child is playing in a playground and wants to walk around a netball court, covering every single line of the court (except the center circle) without leaving the lines at all. The dimensions of the court are as follows:
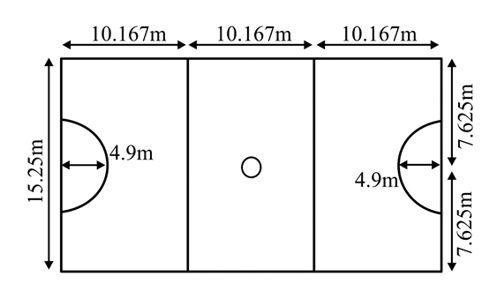
Find the length of each of the semicircular arcs at each end of the court.
A child is playing in a playground and wants to walk around a netball court, covering every single line of the court (except the center circle) without leaving the lines at all. The dimensions of the court are as follows:
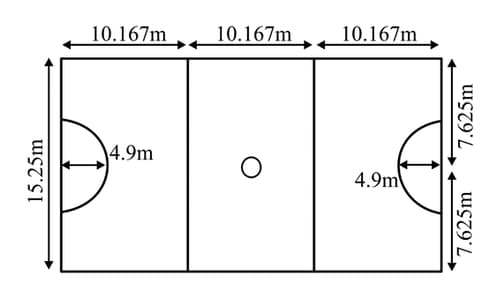
Find the length of each of the semicircular arcs at each end of the court.
Find the shortest distance from the semicircular arc to the corner of the court.
A child is playing in a playground and wants to walk around a netball court, covering every single line of the court (except the center circle) without leaving the lines at all. The dimensions of the court are as follows:
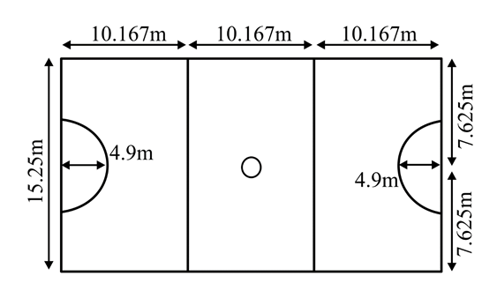
Find the length of each of the semicircular arcs at each end of the court.
Find the shortest distance from the semicircular arc to the corner of the court.
Hence, add weights to this graph to create a network showing the distances between different junctions around the court's edge.
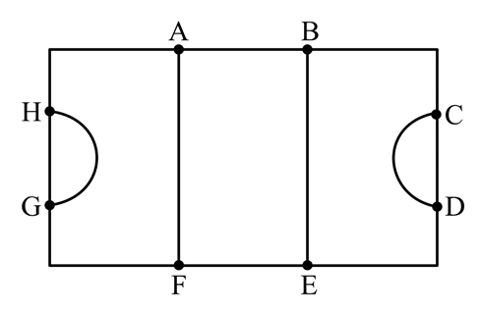
A child is playing in a playground and wants to walk around a netball court, covering every single line of the court (except the center circle) without leaving the lines at all. The dimensions of the court are as follows:

Find the length of each of the semicircular arcs at each end of the court.
Find the shortest distance from the semicircular arc to the corner of the court.
Hence, add weights to this graph to create a network showing the distances between different junctions around the court's edge.

Explain why at least four edges will need to be doubled in order to complete the journey.
A child is playing in a playground and wants to walk around a netball court, covering every single line of the court (except the center circle) without leaving the lines at all. The dimensions of the court are as follows:

Find the length of each of the semicircular arcs at each end of the court.
Find the shortest distance from the semicircular arc to the corner of the court.
Hence, add weights to this graph to create a network showing the distances between different junctions around the court's edge.

Explain why at least four edges will need to be doubled in order to complete the journey.
Write down the four shortest edges in this network along with their weights.
A child is playing in a playground and wants to walk around a netball court, covering every single line of the court (except the center circle) without leaving the lines at all. The dimensions of the court are as follows:

Find the length of each of the semicircular arcs at each end of the court.
Find the shortest distance from the semicircular arc to the corner of the court.
Hence, add weights to this graph to create a network showing the distances between different junctions around the court's edge.

Explain why at least four edges will need to be doubled in order to complete the journey.
Write down the four shortest edges in this network along with their weights.
Hence, give an Eulerian circuit of the least weight for this network. Explain how you can be sure that your circuit is of the least weight without testing other possible routes.
