Rose Harrison, Clara Huizink, Aidan Sproat Clements and, Marlene Torres Skoumal Solutions for Exercise 5: Exploration 2
Rose Harrison Mathematics Solutions for Exercise - Rose Harrison, Clara Huizink, Aidan Sproat Clements and, Marlene Torres Skoumal Solutions for Exercise 5: Exploration 2
Attempt the free practice questions from Exercise 5: Exploration 2 with hints and solutions to strengthen your understanding. Extended MYP Mathematics A Concept based approach Years 4 & 5 solutions are prepared by Experienced Embibe Experts.
Questions from Rose Harrison, Clara Huizink, Aidan Sproat Clements and, Marlene Torres Skoumal Solutions for Exercise 5: Exploration 2 with Hints & Solutions
The probability that it will rain tomorrow is . If it rains tomorrow, the probability that Amanda plays tennis is . If it doesn't rain tomorrow, the probability that she plays tennis is . Let be the event 'rains tomorrow' and be the event 'plays tennis'. Complete the following tree diagram for the events .
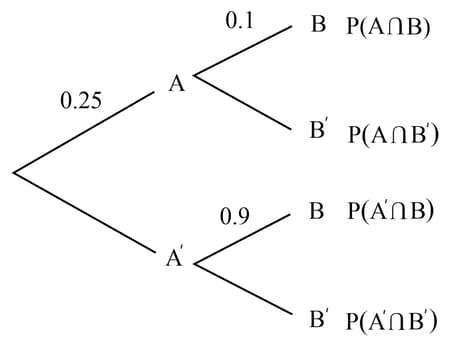
The probability that it will rain tomorrow is . If it rains tomorrow, the probability that Amanda plays tennis is . If it doesn't rain tomorrow, the probability that she plays tennis is . Let be the event 'rains tomorrow' and be the event 'plays tennis'. Complete the following tree diagram for the events . State whether are independent events or not.
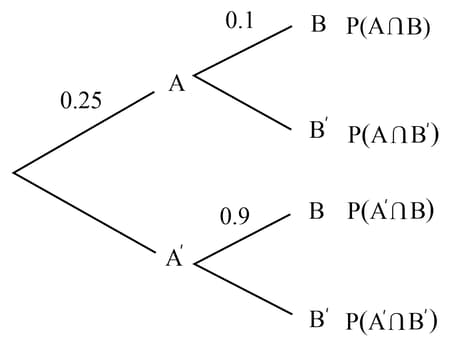
The probability that it will rain tomorrow is . If it rains tomorrow, the probability that Amanda plays tennis is . If it doesn't rain tomorrow, the probability that she plays tennis is . Let be the event 'rains tomorrow' and be the event 'plays tennis'. Complete the following tree diagram for the events . Find the probability that, Amanda plays tennis tomorrow, given that it will be raining
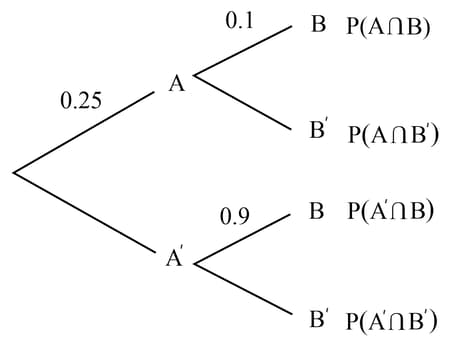
The probability that it will rain tomorrow is . If it rains tomorrow, the probability that Amanda plays tennis is . If it doesn't rain tomorrow, the probability that she plays tennis is . Let be the event 'rains tomorrow' and be the event 'plays tennis'. Find the probability that, Amanda does not play tennis tomorrow, given that it will be raining.
The probability that it will rain tomorrow is . If it rains tomorrow, the probability that Amanda plays tennis is . If it doesn't rain tomorrow, the probability that she plays tennis is . Let be the event 'rains tomorrow' and be the event 'plays tennis'. Find the probability that, Amanda plays tennis tomorrow, given that it will not be raining.
The probability that it will rain tomorrow is . If it rains tomorrow, the probability that Amanda plays tennis is . If it doesn't rain tomorrow, the probability that she plays tennis is . Let be the event 'rains tomorrow' and be the event 'plays tennis'. Find the probability that, Amanda does not play tennis tomorrow, given that it will not be raining.
