S L Arora Solutions for Chapter: Electromagnetic Induction, Exercise 4: HOTS Problem on Higher Order Thinking Skills

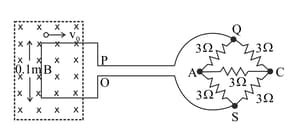
A square metal wire loop of side $10 \mathrm{cm}$ and resistance $1 \mathrm{ohm}$ is moved with a constant velocity $v_0$ in a uniform magnetic field of induction $B=2 \mathrm{Wb} {\mathrm{m}}^{-2}$ as shown in Fig. 6.94. The magnetic lines are perpendicular to the plane of the loop (directed into the paper). The loop is connected to a network of resistors each of value $3 \mathrm{\Omega }$. The resistances of the loop wires $OS$ and $PQ$ are negligible. What should be the speed of the loop so as to have a steady current of $1 \mathrm{mA}$ in the loop? Give the direction of the current in the loop?

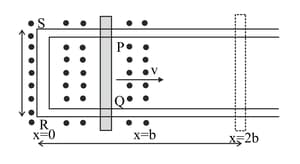
Refer to Fig. 6.95. The arm $PQ$ of the rectangular conductor is moved from $x=0$ to the right side. The uniform magnetic field is perpendicular to the plane and extends from $x=0$ to $x=b$ and is zero for $x>b$. Only the arm $PQ$ possesses substantial resistance $r$. Consider the situation when the arm $PQ$ is pulled outwards from $x=0$ to $x=2 \mathrm{b}$ and is then moved back to $x=0$ with constant speed $v$. Obtain expressions for the flux, the induced emf, the force necessary to pull the arm and the power dissipated as Joule heat. Sketch the variation of these quantities with time.

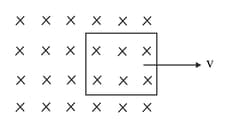
In Fig. 6.97, a square loop has $100$100 turns, an area of $2.5 \times {10}^{-3} {\mathrm{m}}^2$ and a resistance of $100 \mathrm{\Omega }$. The perpendicular magnetic field has a magnitude of $0.40 \mathrm{T}$. If the loop is slowly and uniformly pulled out of the field in $1.0 \mathrm{s}$, find the work done.

A conducting rod $XY$ slides freely on two parallel rails, $A$ and $B$, with a uniform velocity '$v$'. A galvanometer '$G$' is connected, as shown in Fig. 6.98 and the closed circuit has a total resistance '$R$'. A uniform magnetic field, perpendicular to the plane defined by the rails $A$ and $B$ and the rod $XY$ (which are mutually perpendicular), is present over the region, as shown.

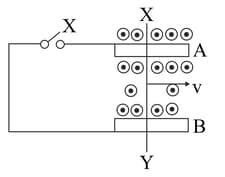
With key $K$ open find the nature of charges developed at the ends of the rod $XY$.

A conducting rod $XY$ slides freely on two parallel rails, $A$ and $B$, with a uniform velocity '$v$'. A galvanometer '$G$' is connected, as shown in Fig. 6.98 and the closed circuit has a total resistance '$R$'. A uniform magnetic field, perpendicular to the plane defined by the rails $A$ and $B$ and the rod $XY$ (which are mutually perpendicular), is present over the region, as shown.

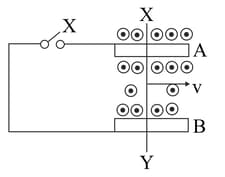
With key $K$ open, Why do the electrons, in the rod $XY$, (finally) experience no net force even though the magnetic force is acting on them due to the motion of the rod?

A conducting rod $XY$ slides freely on two parallel rails, $A$ and $B$, with a uniform velocity '$v$'. A galvanometer '$G$' is connected, as shown in Fig. 6.98 and the closed circuit has a total resistance '$R$'. A uniform magnetic field, perpendicular to the plane defined by the rails $A$ and $B$ and the rod $XY$ (which are mutually perpendicular), is present over the region, as shown.

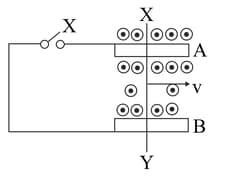
How much power needs to be delivered, (by an external agency), to keep the rod moving at its uniform speed when key $K$ is closed?

A conducting rod $XY$ slides freely on two parallel rails, $A$ and $B$, with a uniform velocity '$v$'. A galvanometer '$G$' is connected, as shown in Fig. 6.98 and the closed circuit has a total resistance '$R$'. A uniform magnetic field, perpendicular to the plane defined by the rails $A$ and $B$ and the rod $XY$ (which are mutually perpendicular), is present over the region, as shown.

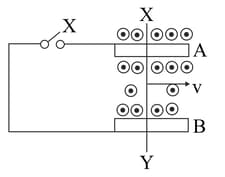
How much power needs to be delivered, (by an external agency), to keep the rod moving at its uniform speed when key $K$ is open?

A conducting rod $XY$ slides freely on two parallel rails, $A$ and $B$, with a uniform velocity '$v$'. A galvanometer '$G$' is connected, as shown in Fig. 6.98 and the closed circuit has a total resistance '$R$'. A uniform magnetic field, perpendicular to the plane defined by the rails $A$ and $B$ and the rod $XY$ (which are mutually perpendicular), is present over the region, as shown.

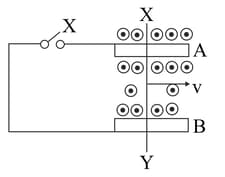
With key $K$ closed, how much power gets dissipated as heat in the circuit? State the source of this power.