Sarvesh K Verma Solutions for Chapter: Theory of Equations, Exercise 16: CAT - Test Questions Helping You Bell the CAT

The equation $\left|x+1\right|\left|x-1\right|=a^2-2a-3$ can have real solutions for $x$, if $a$ belongs to

 If $r$ be the ratio of the roots of the equation $a{x}^2+bx+c=0$, then which one of the following is correct?  

If the roots of the equation ${\mathrm{x}}^2-2\mathrm{ax}+{\mathrm{a}}^2+\mathrm{a}-3=0$ are real and less than $3 ,$ then

If $9\le \mathrm{x}\le 16,$ then

The quadratic equations $\mathrm{f}\left(\mathrm{x}\right)=0$ and $\mathrm{g}\left(\mathrm{x}\right)=0$ have a common root such that $\mathrm{f}\left(2\right)=\mathrm{g}\left(7\right)=0$ and $\mathrm{f}\left(4\right)\times \mathrm{g}\left(9\right)=24.$ Which among the following give (s) all the correct values of the possible common root?

(i) $10,3,-4,-9$

(ii) $-6.5,10,0,-4$

(iii) $-9,-8,-4.5,4$

(iv) $2\sqrt{2},3\sqrt{3},8,27$

(v) $3,10,-5,-8$

If ${\mathrm{P}}_{\mathrm{i}}$ and ${\mathrm{p}}_{\mathrm{i}}$ are the real numbers, then the number of non-real roots of the following equation is
$\frac{{\mathrm{P}}_1^2}{\left(\mathrm{x}-{\mathrm{p}}_1\right)}+\frac{{\mathrm{P}}_2^2}{\left(\mathrm{x}-{\mathrm{p}}_2\right)}+\dots +\frac{{\mathrm{P}}_{\mathrm{k}}^2}{\left(\mathrm{x}-{\mathrm{p}}_{\mathrm{k}}\right)}=\mathrm{x}+1$

If $\mathrm{a}<\mathrm{b}<\mathrm{c}<\mathrm{d}$ and $\mathrm{k}\in \mathrm{R}$, then the roots of the equation $(\mathrm{x}-\mathrm{a})(\mathrm{x}-\mathrm{c})+\mathrm{k}(\mathrm{x}-\mathrm{b})(\mathrm{x}-\mathrm{d})=0$ are

For every $\{\mathrm{b},\mathrm{c}\}\in {\mathrm{R}}^{\oplus }$, the quadratic curve $\mathrm{y}={\mathrm{x}}^2-\mathrm{bx}-\mathrm{c}$ is drawn. The roots are denoted by $\mathrm{A}$ and $\mathrm{B}.$

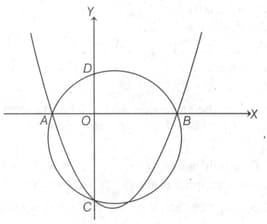
The curve intersects $\mathrm{Y}$-axis at $\mathrm{C}$ and another point $\mathrm{D}$ is taken on the $\mathrm{Y}$-axis such that $\mathrm{A}, \mathrm{D}, \mathrm{B}$ and $\mathrm{C}$ are concyclic. Find the coordinates of $\mathrm{D}.$