Rectangular Cartesian Coordinates of a Point

The points $\left(a+1,1\right),\left(2a+1,3\right)$ and $\left(2a+2,2a\right)$ are collinear, if :

The points $\left(x+1,2\right),\left(1,x+2\right),\left(\frac{1}{x+1},\frac{2}{x+1}\right)$ are collinear, then $x$ is equal to :

If the points $\left(x_1,y_1\right),\left(x_2,y_2\right)$ and $\left(x_3,y_3\right)$ are collinear, show that $\sum \left(\frac{y_1-y_2}{x_1{x}_2}\right)=0$, i.e. $\frac{y_1-y_2}{x_1{x}_2}+\frac{y_2-y_3}{x_2{x}_3}+\frac{y_3-y_1}{x_3{x}_1}=0$

Prove that the points $(a, b),(c, d)$ and $(a-c, b-d)$ are collinear, if $ad=bc$.

Show that if the axes be turned through $7\frac{1°}{2};$ the equation $\sqrt{3}{x}^2+(\sqrt{3}-1)xy-y^2=0$ become free of $xy$ in its new form.

The equation $x^2+2xy+4=0$ is transformed to the parallel axes through the point $(6,\lambda )$. For what value of $\lambda$ its new form passes through the new origin ?

The co-ordinates of three points $O, A, B$ are $(0,0),(0,4)$ and $(6,0)$ respectively. A point $P$ moves so that the area of $∆POA$ is always twice the area of $∆POB$. Find the equation to both parts of the locus of $P$.

The ends of a rod of length $l$ move on two mutually perpendicular lines. Find the locus of the point on the rod which divides it in the ratio $1: 2$.

$OA$ and $OB$ are two perpendicular straight lines. A straight line $AB$ is drawn in such a manner that $OA+OB=8$. Find the locus of the mid point of $AB$.

Use distance formula to show that the points $\left({cosec}^2\alpha ,0\right),\left(0,{\sec }^2\alpha \right)$ and $\left(1,1\right)$ are collinear.

If $\left(3,-4\right)$ and $\left(-6,5\right)$ are the extremities of a diagonal of a parallelogram and $\left(-2,1\right)$ is the third vertex, then its fourth vertex is-

Transform the equation $r=2a\cos \theta$ to Cartesian form.

Transform the equation $y=x\tan \alpha$ to polar form.

A point lies on negative direction of $x$-axis at a distance $6$units from $y$-axis. What are its co-ordinates ?

A point lies on $y$-axis at a distance $4$ units from $x$-axis. What are its co-ordinates ?

A point lies on $x$-axis at a distance $5$ units from $y$-axis. What are its co-ordinates ?

The cartesian co-ordinates of the point $Q$ in the figure is :

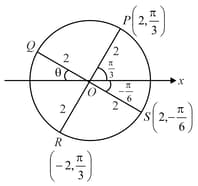
The co-ordinates of $P^{\text{'}}$ in the figure such that $OP=O{P}^{\text{'}}$ is :

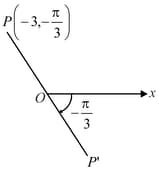
The transform equation of $r^2{\cos }^2\theta =a^2\cos 2\theta$ to Cartesian form is $\left(x^2+y^2\right)x^2=a^2\lambda$, then value of $\lambda$ is :

The Cartesian co-ordinates of the point whose polar co-ordinates are $\left(13,\pi -{\tan }^{-1}\left(\frac{5}{12}\right)\right)$ is :