Section Formula

Find the position vector of a point $P$ which divides the line joining two points $A \& B$, whose position vectors are $\hat{i}+2\hat{j}-\hat{k} \text{and} -\hat{i}+\hat{j}+\hat{k}$, respectively in the ratio of $2:1$ externally.

Let $\overrightarrow{a},\overrightarrow{b}$ and $\overrightarrow{c}$ be three non-zero vectors such that no two of these are collinear. If the vector $\overrightarrow{a}+2\overrightarrow{b}$ is collinear with $\overrightarrow{c}$ and $\overrightarrow{b}+3\overrightarrow{c}$ is collinear with $\overrightarrow{a}$ ($\lambda$ being some non-zero scalar), then $\overrightarrow{a}+2\overrightarrow{b}+6\overrightarrow{c}$ equals

If $C$ is the midpoint of $AB$ and $P$ is any point outside $B$, then

The position vectors of $\overrightarrow{A}$ and $\overrightarrow{B}$ are $\hat{i}–\hat{j}+2\hat{k}$ and $3\hat{i}–\hat{j}+3\hat{k}$. The position vector of the middle point of the line $\overrightarrow{AB}$ is

If the position vectors of the points $\overrightarrow{A}$ and $\overrightarrow{B}$ are $\hat{i}+3\hat{j}–\hat{k}$ and $3\hat{i}–\hat{j}– 3\hat{k}$, then what will be the position vector of the midpoint of $\overrightarrow{AB}$.

If $O$ is origin and $C$ is the mid-point of $A(2,-1)$ and $B(-4,3)$. Then, value of $\overrightarrow{OC}$ is

The position vector of the points which divides internally in the ratio$2 :3$ the join of the points $\left(2\overrightarrow{a} – 3\overrightarrow{b}\right)$and $\left(3\overrightarrow{a} –2\overrightarrow{b}\right)$, is

If $\overrightarrow{a}$ and $\overrightarrow{b}$ are position vector of two points $A,B$ and $C$ divides $\overrightarrow{AB}$ in ratio $2:1$, then position vector of $C$ is

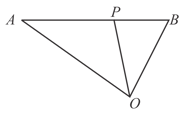
If in the given figure, $\overrightarrow{OA}=\overrightarrow{a}, \overrightarrow{OB}=\overrightarrow{b}$ and $\overrightarrow{AP}:\overrightarrow{PB}=m:n$, then $\overrightarrow{OP}$ is equal to

Points $X \mathrm{and} Y$ are taken on the sides $\overrightarrow{QR} \mathrm{and} \overrightarrow{RS}$, respectively of a parallelogram $PQRS$, so that $\overrightarrow{QX}=4\overrightarrow{XR} \mathrm{and} \overrightarrow{RY}=4\overrightarrow{YS}$. The line $\overrightarrow{XY}$ cuts the line $\overrightarrow{PR}$ at $Z$. Then, $\overrightarrow{PZ}$ is

In the $\Delta OAB$, $M$ is the mid-point of $\overrightarrow{AB}$,$C$ is a point on $\overrightarrow{OM}$, such that $2\overrightarrow{OC}=\overrightarrow{CM}$. $X$ is a point on the side $\overrightarrow{OB}$ such that $\overrightarrow{OX}=2\overrightarrow{XB}$. The line $\overrightarrow{XC}$ is produced to meet $\overrightarrow{OA}$ in $Y$. Then, $\frac{\overrightarrow{OY}}{\overrightarrow{YA}}$ is equal to

$ABCD$ is a quadrilateral. $E$ is the point of intersection of the line joining the midpoints of the opposite sides. If $O$ is any point and $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=x\overrightarrow{OE}$, then $x$ is equal to

The position vectors of the points $P$ and $Q$ with respect to the origin $O$ are $\overrightarrow{a }=\hat{i}+3 \hat{j}-2 \hat{k}$ and $\overrightarrow{b }=3 \hat{i}-\hat{j}-2 \hat{k}$, respectively. If $M$ is a point on $\overrightarrow{PQ}$, such that $\overrightarrow{OM}$ is the bisector of $\angle POQ$, then $\overrightarrow{OM }$ is

$A,B,C \mathrm{and} D$ have position vectors $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c} \mathrm{and} \overrightarrow{d}$, respectively, such that $\overrightarrow{a}–\overrightarrow{b}=2\left(\overrightarrow{d}–\overrightarrow{c}\right)$. Then,

If $4\hat{j}+7\hat{j}+8\hat{k}, 2\hat{i}+3\hat{j}+4\hat{k}$ and $2\hat{\mathrm{i}}+5\hat{j}+7\hat{k}$ are the position vectors of the vertices $A,B \mathrm{and} C$, respectively of $\Delta ABC$. The position vector of the point where the bisector of $\angle A$ meets $\overrightarrow{BC}$ is

If $\overrightarrow{b}$ is a vector whose initial point divides the join of $\mathrm{5}\hat{i}$ and $5\hat{j}$ in the ratio $k:1$ and whose terminal point is origin and $\left|\overrightarrow{b}\right|$$\le \sqrt{37}$, then $k$ lies in the interval

If in a triangle, $\overrightarrow{AB}=\overrightarrow{a}, \overrightarrow{AC}=\overrightarrow{b} \text{and} D,E$ are the midpoints of $\overrightarrow{AB} \text{and} \overrightarrow{AC}$, respectively, then $\overrightarrow{DE}$ is equal to

If three points $A,B \text{and} C$ are collinear, whose position vectors are $\hat{i}–2\hat{j}-8\hat{k}, 5\hat{i}–2\hat{k}$ and $11\hat{i}+3\hat{j}+7\hat{k}$, respectively, then the ratio in which $B$ divides $\overrightarrow{AC}$ is

$A \text{and} B$ are two points. The Position Vector of $A$ is $6\overrightarrow{b}–2\overrightarrow{a}$. A Point $P$ divides the line $\overrightarrow{AB}$ in the ratio $1:2.$ If  $\overrightarrow{a}–\overrightarrow{b}$ is the position vector of $P$, then the position vector of $B$ is given by

If the position vector of one end of a line segment $\overrightarrow{AB}$ is $2\hat{i}+3\hat{j}-\hat{k}$ and the position vector of its middle point is $3\left(\hat{i}+\hat{j}+\hat{k}\right)$, then find the position vector of the other end.