Triangle Speciality

A point inside a quadrilateral is joined to its vertices and the lines are extended by the same scale factor. Their ends are joined to make another quadrilateral.

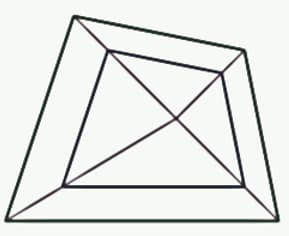
Prove that the angles of the two quadrilaterals are the same.

A point inside a quadrilateral is joined to its vertices and the lines are extended by the same scale factor. Their ends are joined to make another quadrilateral.

Prove that the sides of the two quadrilateral are scaled by the same factor.

The lines joining the circumcentre of a triangle to the vertices are extended to meet another circle with the same centre, and these points are joined to make another triangle.

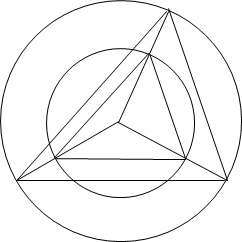
Prove that the scale factor of the sides of the triangle is the scale factor of the radii of the circles.

The lines joining the circumcentre of a triangle to the vertices are extended to meet another circle with the same centre, and these points are joined to make another triangle.

Prove that the two triangles are similar.

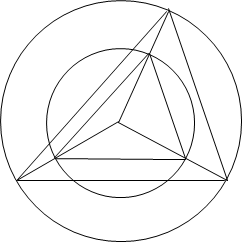
The picture shows two circles with the same centre and two triangles formed by joining the centre to the points of intersection of the circles with two radii of the larger circle:

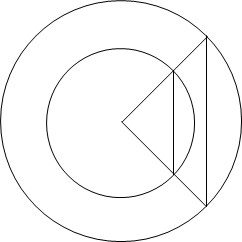
Prove that these triangles are similar.

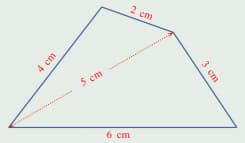
See this picture of a quadrilateral.

Draw a quadrilateral with angles different from those of this and sides scaled by $1\frac{1}{2}$.

See this picture of a quadrilateral.

Draw a quadrilateral with angles the same as those of this one and sides scaled by $1\frac{1}{2}$.

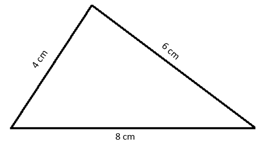
Draw a triangle of angles the same as those of the triangle shown and sides scaled by $1\frac{1}{4}$.

Two poles of heights $3 \mathrm{m}$ and $2 \mathrm{m}$ are erected upright on the ground and ropes are stretched from the top of each to the foot of the other.

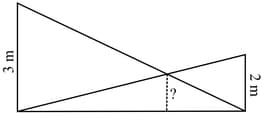
Prove that this height would be the same, whatever be the distance between the poles.

Two poles of heights $3 \mathrm{m}$ and $2 \mathrm{m}$ are erected upright on the ground and ropes are stretched from the top of each to the foot of the other.

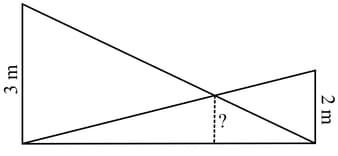
Taking the height of the poles as $a$ and $b$ and height above the ground of the point where the ropes cross each other as $h$, find the relation between $a, b$ and $h$.

Two poles of heights $3 \mathrm{m}$ and $2 \mathrm{m}$ are erected upright on the ground and ropes are stretched from the top of each to the foot of the other.

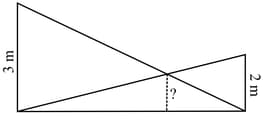
At what height  above the ground do the ropes cross each other?

The picture shows a square drawn sharing one corner with a right triangle and the other three corners on the sides of this triangle.

What is the length of a side of the square drawn like this within a triangle of sides $3 \mathrm{cm}, 4 \mathrm{cm}$ and $5 \mathrm{cm}$.

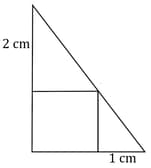
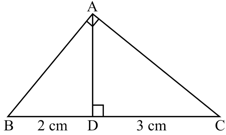
The perpendicular from the square corner of a right-triangle divides the opposite side into two parts of lengths $a$ and $b$. Taking the length of the perpendicular as $h$, prove that $h^2=ab$.

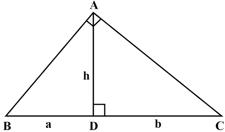
The perpendicular from the square corner of a right-triangle cuts the opposite side into two parts of $2$ and $3$ centimetres of length. Calculate the perpendicular sides of the large triangle.

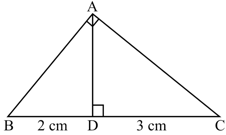
The perpendicular from the square corner of a right-triangle cuts the opposite side into two parts of $2$ and $3 \mathrm{centimetres}$ of length. Taking the length of the perpendicular as $h$, prove that $\frac{h}{2}=\frac{3}{h}$.

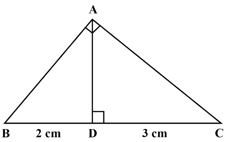
The perpendicular from the square corner of a right-triangle cuts the opposite side into two parts of $2$ and $3$ $\mathrm{centimetres}$ of length. Prove that the two small right triangles cut by the perpendicular have the same angles.