The equation of a curve y = 3 + 4 x - x 2 passes through the point A 3 , 6 . Find the coordinates of the point B at which the normal meets the curve again.

Given, y = 3 + 4 x - x 2 . . . . . . . i ∴ d y d x = 0 + 4 - 2 x ⇒ d y d x = 4 - 2 x When x = 3 , d y d x = 4 - 6 = - 2 Normal at A : passes through the point 3 , 6 and gradient = 1 2 y - 6 = 1 2 x - 3 ⇒ y = x 2 - 3 2 + 6 ⇒ y = x 2 + 9 2 . . . . . . . i i Equating equations i and i i , we get 3 + 4 x - x 2 = x 2 + 9 2 ⇒ 2 3 + 4 x - x 2 = x + 9 ⇒ 6 + 8 x - 2 x 2 = x + 9 ⇒ 2 x 2 - 7 x + 3 = 0 ⇒ x - 3 2 x - 1 = 0 Solving gives x = 3 and x = 1 2 Given the point 3 , 6 so we have to consider x = 1 2 , y = 3 + 4 1 2 - 1 4 = 5 - 1 4 = 19 4 = 4 3 4 ∴ The coordinates of the point B are 1 2 , 4 3 4

Sue Pemberton Solutions for Chapter: Differentiation, Exercise 6: END-OF-CHAPTER REVIEW EXERCISE 7

Author:Sue Pemberton

Sue Pemberton Mathematics Solutions for Exercise - Sue Pemberton Solutions for Chapter: Differentiation, Exercise 6: END-OF-CHAPTER REVIEW EXERCISE 7

Attempt the practice questions on Chapter 7: Differentiation, Exercise 6: END-OF-CHAPTER REVIEW EXERCISE 7 with hints and solutions to strengthen your understanding. Cambridge International AS & A Level Mathematics : Pure Mathematics 1 Course Book solutions are prepared by Experienced Embibe Experts.

Questions from Sue Pemberton Solutions for Chapter: Differentiation, Exercise 6: END-OF-CHAPTER REVIEW EXERCISE 7 with Hints & Solutions

MEDIUM

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 1 Course Book>Chapter 7 - Differentiation>END-OF-CHAPTER REVIEW EXERCISE 7>Q 13

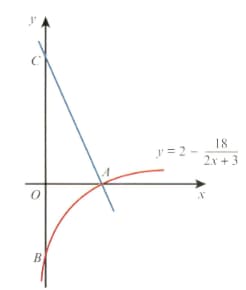
Question Image

The diagram shows part of the curve $y = 2 - \frac{18}{2 x + 3}$ , which crosses the $x -$ axis at $A$ and the $y -$ axis at $B$ .

The normal to the curve at $A$ crosses the $y -$ axis at $\frac{d u}{d x} = 2 (1) + 0 = 2$ .

Show that the equation of the line $A C$ is $9 x + 4 y = 27$ .

MEDIUM

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 1 Course Book>Chapter 7 - Differentiation>END-OF-CHAPTER REVIEW EXERCISE 7>Q 13

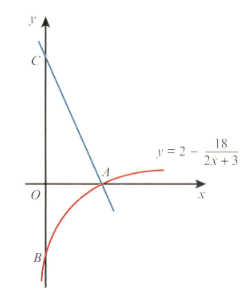
Question Image

The diagram shows part of the curve $y = 2 - \frac{18}{2 x + 3}$ , which crosses the $x -$ axis at $A$ and the $y -$ axis at $B$ .

The normal to the curve at $A$ crosses the $y -$ axis at $C$ .

Find the length of $B C$ .

EASY

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 1 Course Book>Chapter 7 - Differentiation>END-OF-CHAPTER REVIEW EXERCISE 7>Q 14

The equation of a curve is $y = 3 + 4 x - x^{2}$ .

Show that the equation of the normal to the curve at the point $(3, 6)$ is $2 y = x + 9$ .

EASY

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 1 Course Book>Chapter 7 - Differentiation>END-OF-CHAPTER REVIEW EXERCISE 7>Q 14

The equation of a curve is $y = 3 + 4 x - x^{2}$ .

Show that the equation of the normal to the curve at the point $(3, 6)$ is $2 y = x + 9$ .

Given that the normal meets the coordinate axes at points $A$ and $B$ , find the coordinates of the mid-point of $A B$ .

EASY

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 1 Course Book>Chapter 7 - Differentiation>END-OF-CHAPTER REVIEW EXERCISE 7>Q 14

The equation of a curve $y = 3 + 4 x - x^{2}$ passes through the point $9 x + 4 y = 27$ .

Find the coordinates of the point $B$ at which the normal meets the curve again.

EASY

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 1 Course Book>Chapter 7 - Differentiation>END-OF-CHAPTER REVIEW EXERCISE 7>Q 15

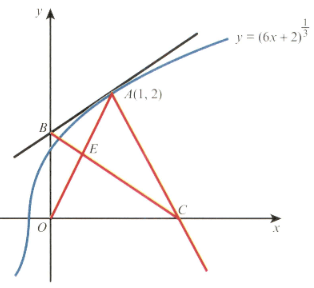
Question Image

The diagram shows the curve $y = {(6 x + 2)}^{\frac{1}{3}}$ and the point $A (1, 2)$ which lies on the curve. The tangent to the curve at $A$ cuts the $y -$ axis at $B$ and the normal to the curve at $A$ cuts the $x -$ axis at $C$ .

Find the equation of the tangent $A B$ and the equation of the normal $A C$ .

MEDIUM

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 1 Course Book>Chapter 7 - Differentiation>END-OF-CHAPTER REVIEW EXERCISE 7>Q 15

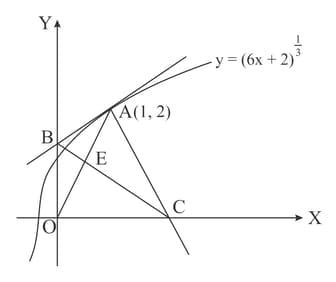
Question Image

Find the distance $B C .$

HARD

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 1 Course Book>Chapter 7 - Differentiation>END-OF-CHAPTER REVIEW EXERCISE 7>Q 15

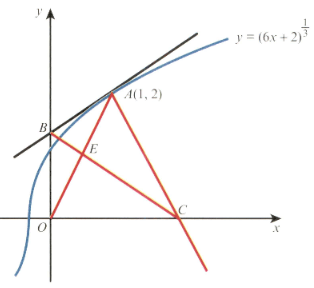
Question Image

Find the coordinates of the point of intersection, $E$ , of $O A$ and $B C$ , and determine whether $E$ is the mid-point of $O A$ .

Sue Pemberton Solutions for Chapter: Differentiation, Exercise 6: END-OF-CHAPTER REVIEW EXERCISE 7

Sue Pemberton Mathematics Solutions for Exercise - Sue Pemberton Solutions for Chapter: Differentiation, Exercise 6: END-OF-CHAPTER REVIEW EXERCISE 7

Questions from Sue Pemberton Solutions for Chapter: Differentiation, Exercise 6: END-OF-CHAPTER REVIEW EXERCISE 7 with Hints & Solutions

Learn and Prepare for any exam you want !