Sue Pemberton Solutions for Chapter: Integration, Exercise 10: END-OF-CHAPTER REVIEW EXERCISE 9

The function $f$ is such that $f^{\text{'}}\left(x\right)=12x^3+10x$ and $f(-1)=1$. Find $f\left(x\right)$

Find $\int {\left(5x-\frac{2}{x}\right)}^2 dx$.

A curve is such that $\frac{dy}{ dx}=\frac{6}{x^2}-5x$ and the point $(3,5.5)$ lies on the curve. Find the equation of the curve.

A curve has equation $y=f\left(x\right)$. It is given that $f^{\text{'}}\left(x\right)=\frac{3}{\sqrt{x+2}}-\frac{8}{x^3}$ and that $f\left(2\right)=3$. Find $f\left(x\right)$.

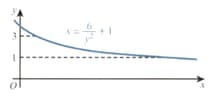
The diagram shows part of the curve $x=\frac{6}{y^2}+1$. The shaded region is bounded by the curve, the $y-$axis, and the lines $y=1$ and $y=3$. Find the volume, in terms of $\pi$, when this shaded region is rotated through $360°$ about the $y-$axis is of the form of $\frac{k\mathrm{\pi }}{9} unit{s}^3$, then $k=$

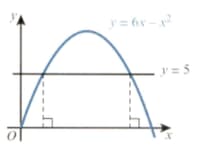
The diagram shows the curve $y=6x-x^2$ and the line $y=5$. Find the area of the shaded region.     [Enter the value excluding units]

Sketch the curve $y=(x-3{)}^2+2$.

The region enclosed by the curve $y=(x-3{)}^2+2$, the $x-$axis, the $y-$axis, the line $x=3$ is rotated through $360°$ about the $x-$axis. Find the volume obtained, giving your answer in terms of $\pi$ is of the form of $\frac{k\mathrm{\pi }}{5}$, then $k=$