Sue Pemberton, Julianne Hughes and, Julian Gilbey Solutions for Chapter: Cross-Topic Review Exercise 4, Exercise 1: CROSS-TOPIC REVIEW EXERCISE 4

Relative to the origin $O,$ the position vectors of the points $A$ and $B$ are given by $\overrightarrow{OA}=\left(\begin{array}{r}-5\\ 0\\ 3\end{array}\right)$ and $\overrightarrow{OB}=\left(\begin{array}{l}1\\ 7\\ 2\end{array}\right)$
Find a vector equation of the line $AB.$

The line $AB$ is perpendicular to the line $L$ with vector equation:

$\overrightarrow{r}=\left(\begin{array}{r}4\\ 2\\ -3\end{array}\right)+\mu \left(\begin{array}{c}m\\ 3\\ 9\end{array}\right)$

Find the value of $m.$

The line $L_1$ has a vector equation

$r=-2\hat{j}+\hat{k}+\lambda \left(\hat{i}+3\hat{k}\right)$

The line $L_2$ passes through the point $P\left(-2, 1, -1\right)$ and is parallel to $L_1.$

Find the shortest distance from $P$ to the line $L_1$.

In a certain country the government charges tax on each litre of petrol sold to motorists. The revenue per year is $R$ million dollars when the rate of tax is $x$ dollars per litre. The variation of $R$ with $x$ is modelled by the differential equation $\frac{\mathrm{d}R}{\mathrm{d}x}=R\left(\frac{1}{x}-0.57\right),$

where $R$ and $x$ are taken to be continuous variables. When $x=0.5, R=16.8$.

This model predicts that $R$ cannot exceed a certain amount. Find this maximum value of $R$.

(Use $\ln \left(16.8\right)=2.82, \ln \left(0.5\right)=-0.693$)

The complex number $z$ is defined by $z=\frac{9\sqrt{3}+9\mathrm{i}}{\sqrt{3}-\mathrm{i}}.$ Find the two square roots of $z,$ giving your answers in the form $r{e}^{\mathrm{i}\theta },$ where $r>0$ and $-\pi <\theta ⩽\pi$.

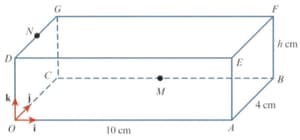
The diagram shows a cuboid $OABCDEFG$ with a horizontal base $OABC$. The cuboid has a length $OA$ of $10 \mathrm{cm},$ a width $AB$ of $4 \mathrm{cm}$ and a height $BF$ of $h \mathrm{cm}.$ The point $M$ is the midpoint of $CB$ and the point $N$ is the point on $DG$ such that $\overrightarrow{ON}=\mathrm{j}+3\mathrm{k}.$ The unit vectors $\mathrm{i}, \mathrm{j}$ and $\mathrm{k}$ are parallel to $OA, OC$ and $OD,$ respectively.

Write down the value of $h.$

The variables $x$ and $y$ are related by the differential equation $\frac{\mathrm{d}y}{ \mathrm{d}x}=\frac{6x{\mathrm{e}}^{3x}}{y^2}.$

It is given that $y=2$ when $x=0.$ Solve the differential equation and hence find the value of $y$ when $x=0.5,$ giving your answer correct to $2$ decimal places.

The line $L_1$ has vector equation $\mathbf{r}=\left(\begin{array}{r}-2\\ 3\\ 0\end{array}\right)+\lambda \left(\begin{array}{r}1\\ -1\\ 2\end{array}\right).$
The line $L_2$ has vector equation $\mathbf{r}=\left(\begin{array}{r}-4\\ 5\\ m\end{array}\right)+\mu \left(\begin{array}{r}-1\\ 0\\ 1\end{array}\right).$

Find the value of $m$ in the case where $L_1$ and $L_2$ intersect.

The number of birds of a certain species in a forested region is recorded over several years. At time $t$ years, the number of birds is $N,$ where $N$ is treated as a continuous variable.
The variation in the number of birds is modelled by $\frac{\mathrm{d}N}{ \mathrm{d}t}=\frac{N(1800-N)}{3600}.$ It is given that $N=300$ when $t=0.$

According to the model, how many birds will there be after a long time?