In triangle A B C , X and Y are the midpoints of A B and A C , respectively. A X → = a and A P → = b . Use a vector method to prove that B C is parallel to X Y .

Given that: A X → = a and A P → = b . We have to prove that B C is parallel to X Y . In triangle A B C , X and Y are the midpoints of A B and A C , respectively. So, X Y → = b - a and B C → = 2 b - 2 a = 2 b - a Thus, B C → = 2 X Y → B C → is a scalar multiple of X Y → Therefore, B C → parallel to X Y → . Hence, proved.

A B C D E F G H is a regular octagon. A B → = p , A H → = q , H G → = r and H C → = s . Using the vectors p , q , r and s , write down expressions for B C → .

Given that: A B → = p , A H → = q , H G → = r and H C → = s . We have to write down expressions for B C → . B C → is the resultant vector formed from A B → + A H → + H C → So, B C → = A B → + A H → + H C → ⇒ B C → = A H → + H C → - B A → ⇒ B C → = q + s - p Hence, B C → = q + s - p

A B C D E F G H is a regular octagon. A B → = p , A H → = q , H G → = r and H C → = s . Using the vectors p , q , r and s , write down expressions for E B → .

Given that: A B → = p , A H → = q , H G → = r and H C → = s . We have to write down expressions for B C → . B C → is the resultant vector formed from A B → + A H → + H C → So, B C → = A B → + A H → + H C → ⇒ B C → = A H → + H C → - B A → ⇒ B C → = q + s - p Hence, B C → = q + s - p Now, E B → is the resultant vector formed from B C → + C D → + D E → So, E B → = B C → + C D → + D E → ⇒ E B → = q + s - p + r + q ⇒ E B → = 2 q + s + r - p Hence, E B → = 2 q + s + r - p .

Sue Pemberton, Julianne Hughes and, Julian Gilbey Solutions for Chapter: Vectors, Exercise 3: EXERCISE 9A

Author:Sue Pemberton, Julianne Hughes & Julian Gilbey

Sue Pemberton Mathematics Solutions for Exercise - Sue Pemberton, Julianne Hughes and, Julian Gilbey Solutions for Chapter: Vectors, Exercise 3: EXERCISE 9A

Attempt the free practice questions on Chapter 9: Vectors, Exercise 3: EXERCISE 9A with hints and solutions to strengthen your understanding. Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book solutions are prepared by Experienced Embibe Experts.

Questions from Sue Pemberton, Julianne Hughes and, Julian Gilbey Solutions for Chapter: Vectors, Exercise 3: EXERCISE 9A with Hints & Solutions

HARD

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 9 - Vectors>EXERCISE 9A>Q 4

In triangle $A B C, X$ and $Y$ are the midpoints of $A B$ and $A C,$ respectively.

$\vec{A X} = a$ and $\vec{A P} = b .$

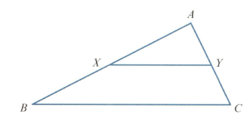
Question Image

Use a vector method to prove that $B C$ is parallel to $X Y .$

HARD

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 9 - Vectors>EXERCISE 9A>Q 4

In triangle $A B C, X$ and $Y$ are the midpoints of $A B$ and $A C,$ respectively.

$\vec{A X} = a$ and $\vec{A P} = b .$

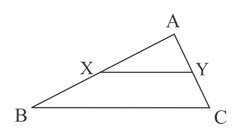
Question Image

$| \vec{X Y} | = k | \vec{B C} |$
Write down the value of the constant $k .$

HARD

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 9 - Vectors>EXERCISE 9A>Q 5

The diagram shows a cuboid, $A B C D E F G H .$

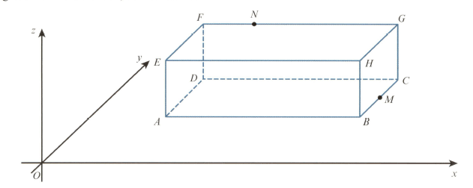
Question Image

$M$ is the midpoint of $B C$ and the point $N$ is on $F G$ such that $F N : N G$ is $1 : 3 .$ Given that $\vec{A G} = (\begin{matrix} 12 \\ 4 \\ 2 \end{matrix}),$ find the displacement vector:

$\vec{A M}$

HARD

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 9 - Vectors>EXERCISE 9A>Q 5

The diagram shows a cuboid, $A B C D E F G H .$

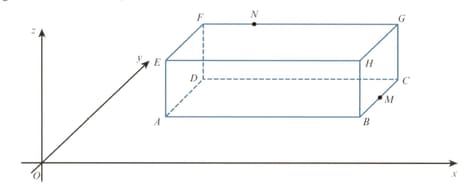
Question Image

$M$ is the midpoint of $B C$ and the point $N$ is on $F G$ such that $F N : N G$ is $1 : 3 .$ Given that $\vec{A G} = (\begin{matrix} 12 \\ 4 \\ 2 \end{matrix}),$ find the displacement vector:

$\vec{A N} .$

HARD

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 9 - Vectors>EXERCISE 9A>Q 6

$A B C D E F G H$ is a regular octagon. $\vec{A B} = p, \vec{A H} = q, \vec{H G} = r$ and $\vec{H C} = s .$

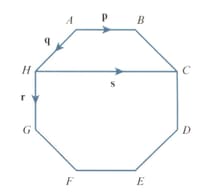
Question Image

Using the vectors $p, q, r$ and $s,$ write down expressions for $\vec{B C}$ .

HARD

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 9 - Vectors>EXERCISE 9A>Q 6

$A B C D E F G H$ is a regular octagon. $\vec{A B} = p, \vec{A H} = q, \vec{H G} = r$ and $\vec{H C} = s .$

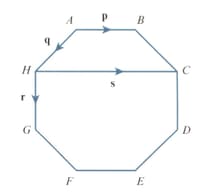
Question Image

Using the vectors $p, q, r$ and $s,$ write down expressions for $\vec{E B}$ .

HARD

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 9 - Vectors>EXERCISE 9A>Q 6

$A B C D E F G H$ is a regular octagon. $\vec{A B} = p, \vec{A H} = q, \vec{H G} = r$ , $\vec{H C} = s$

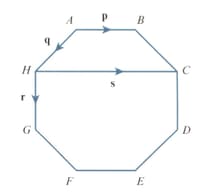
Question Image

and $s = (1 + \sqrt{k}) p$ then find the exact value of $k .$

MEDIUM

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 9 - Vectors>EXERCISE 9A>Q 7

Use a vector method to show that, when the diagonals of a quadrilateral bisect one another, then the opposite sides are parallel and equal in length.

Sue Pemberton, Julianne Hughes and, Julian Gilbey Solutions for Chapter: Vectors, Exercise 3: EXERCISE 9A

Sue Pemberton Mathematics Solutions for Exercise - Sue Pemberton, Julianne Hughes and, Julian Gilbey Solutions for Chapter: Vectors, Exercise 3: EXERCISE 9A

Questions from Sue Pemberton, Julianne Hughes and, Julian Gilbey Solutions for Chapter: Vectors, Exercise 3: EXERCISE 9A with Hints & Solutions

Learn and Prepare for any exam you want !