Umakant Kondapure, Collin Fernandes, Nipun Bhatia, Vikram Bathula and, Ketki Deshpande Solutions for Chapter: Rotational Motion, Exercise 4: Evaluation Test

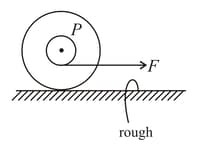
Consider a yo-yo kept vertically on the floor. Its inner and outer radii are $r \text{and} R$, respectively. A thread is wound over its inner surface and placed over a rough horizontal surface. Thread is pulled over by a force $F$. In case of

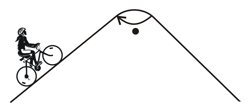
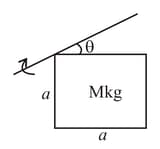
A bicycle is going up on the mountain as shown in the diagram. What can we conclude about the direction of friction?

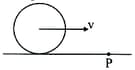
In a bowling event, a ball is thrown with a velocity $v$on a horizontal track. However, the ball suddenly encounters a chewing gum. The spherical ball sticks to the point and does pure rotation. Find the angular velocity of the ball as soon as it starts pure rotation.

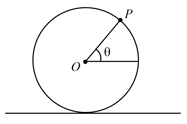
A disc is in pure rolling motion with a velocity $v$ on a rough horizontal surface. The resultant velocity of a point $P$ at an angle $\theta$ with the horizontal would be

A square plate of side $a=20 \mathrm{cm}$ and mass $M=2 \mathrm{kg}$ is lying on the horizontal plane. What will be the moment of inertia of the plate about an axis in the plane of the plate and at an angle of $\theta =18.6°$ from one of its sides?

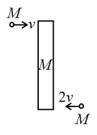
Two masses $\left(M\right)$ are moving perpendicular to the rod of mass $M$ with velocities $v\text{ and} 2v$ as shown in the figure. The length of the rod is $L$. Find the ratio of the final velocity of the rod and its angular velocity if the masses stop at their place after collision.

A thin rod is placed co-axially within a thin hollow tube which lies on a smooth horizontal table. The rod having the same mass ' $M$ ' and length '$L$' as that of the tube is free to move within the tube. The system is given an angular velocity ' $\omega$ ' about a vertical axis from one of its ends. Considering negligible friction between surfaces, find the angular velocity of the rod as it just slips out of the tube.
 

A sphere rolls on the surface with velocity $v$. It encounters a smooth frictionless incline of height $h$ which it needs to climb. What will be the minimum velocity for which it will climb the incline?