Umakant Kondapure, Collin Fernandes, Nipun Bhatia, Vikram Bathula and, Ketki Deshpande Solutions for Chapter: Electromagnetic Induction, Exercise 4: Evaluation Test

A cylindrical region of uniform magnetic field exists perpendicular to plane of paper which is increasing at a constant rate $\frac{\mathrm{d}B}{\mathrm{d}t}=\alpha$. The diameter of cylindrical region is $l$. A non-conducting rigid rod of length $l$ having two charged particles is kept fixed on the diameter of cylindrical region w.r.t. inertial frame. If two charged particles, having charges $\overline{q}$ each, is kept fixed at the ends of non-conducting rod, the net force on any one of the charge is,

A square frame with side $a$ and a straight conductor carrying a constant current $I$ are located in the same plane. The resistance of the frame is equal to $R$. The frame was turned through $180°$ about the axis $O{O}^{\mathit{\text{'}}}$ separated from the current-carrying conductor by a distance, $b=2a$. If the electric charge that flowed through the frame be expressed as a function of $a$, $I$, $R$, it takes the form, $q\mathit{=}\text{constant}\times a^{\mathrm{m}}\times I^{\mathrm{n}}\times R^{\text{p}}$. Find $m+n+p$.
 

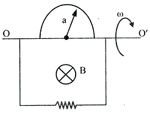
A wire shaped as a semi-circle of radius $a$ rotates about an axis ${\mathrm{OO}}^{\text{'}}$ with an angular velocity $\omega$ in a uniform magnetic field of induction $B$ (shown in figure). The axis of rotation is perpendicular to the field direction. The total resistance of the circuit is equal to $R$. Neglecting the magnetic field of induced current, calculate the mean amount of thermal power being generated in the loop during one rotation period and express it in the form:
$P_{\text{mean}}=B^{\mathrm{m}}{a}^{\mathrm{n}}{\omega }^{\mathrm{p}}\times$ constant. Find the value of $P$.

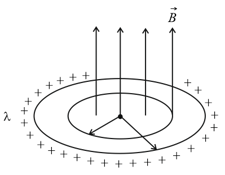
A ring of mass $m$, radius $r$ with charge per unit length $\lambda$ encloses a magnetic field such that, $B=-B_0\hat{\mathrm{k}}$ when $r\le a \& B=0$ when $r>a$. When the magnetic field is switched off, the rings starts to rotate due to induced electric field with varying flux. Find angular velocity (in${10}^{-2} \mathrm{rad} {\mathrm{s}}^{-1}$) with which the ring rotates after the magnetic field has been completely turned off. ($B_0=1 \mathrm{T}$, $a=1 \mathrm{cm}\text{,} r=2 \mathrm{cm}\text{,} m=0.5 \mathrm{kg}$, $\lambda =\frac{4}{\pi } \mathrm{C} {\mathrm{m}}^{-1}$)

Two vertical rails are connected at the ends with a capacitor. There is a magnetic field $\overrightarrow{B}$ directed horizontally. A wire of mass $m$ slides down the rails. Find the acceleration of wire, given that mass $m=1 \mathrm{kg}\text{,} g=10 \mathrm{m} {\mathrm{s}}^{-2}$, $B=1 \mathrm{T}$, length of wire$=1 \mathrm{m}$, capacitance, $C=1 \mathrm{F}$. (The wire and the rails offer zero electrical resistance.)

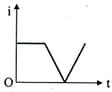
The current in an induction coil varies with time $t$ according to the graph shown in the figure. Which of the following graphs shows variation of induced e.m.f. $\left(e\right)$ in coil with time?

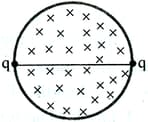
A ring of mass $4 \mathrm{kg}$ is uniformly charged with $\lambda =4 \mathrm{C} {\mathrm{m}}^{-1}$ and kept on a rough horizontal surface with frictional coefficient, $\mu =\frac{\pi }{4}$. Time-varying magnetic field, $B=B_0{t}^2$ is applied on a circular region of radius $a (a<r)$ perpendicular to plane of ring as shown in figure. Find out the time when the ring just starts to rotate on surface. (Given, $a=5 \mathrm{cm}, g=10 \mathrm{m} {\mathrm{s}}^{-2}, B_0=125 \text{S.I.}$ units.)

The current in coil changes from $0.5 \mathrm{A}$ to $2 \mathrm{A}$ in $0.03 \mathrm{s}$ inducing a voltage of $8 \mathrm{V}$ across it. Find initial energy stored in the coil.