Umakant Kondapure, Collin Fernandes, Nipun Bhatia, Vikram Bathula and, Ketki Deshpande Solutions for Chapter: Kinetic Theory of Gases and Radiations, Exercise 3: Competitive Thinking

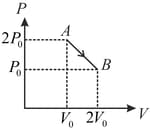
$n$ moles of an ideal gas undergoes a process $A\to B$ as shown in the figure. The maximum temperature of the gas during the process will be

The amount of heat energy required to raise the temperature of $1 \mathrm{g}$ of Helium at N.T.P., from $T_1$ to $T_2$ is 

At what temperature will the RMS speed of oxygen molecules become just sufficient for escaping from the Earth's atmosphere? (Given: Mass of oxygen molecule $m=2.76\times {10}^{-26} \mathrm{kg}$, Boltzmann's constant $k_{\mathrm{B}}=1.38\times {10}^{-23} \mathrm{J} {\mathrm{K}}^{-1}$

Assertion: Thermodynamic processes in nature are irreversible.

Reason: Dissipative effects cannot be eliminated.

Assertion: In an isolated system, the entropy increases.

Reason: The processes in an isolated system are adiabatic.

One mole of an ideal gas requires $207 \mathrm{J}$ heat to raise the temperature by $10 \mathrm{K}$ when heated at constant pressure. If the same gas is heated at constant volume to raise the temperature by $10 \mathrm{K}$ then heat required is [given gas constant $R=8.3 \mathrm{J} {\mathrm{mol}}^{-1} {\mathrm{K}}^{-1}$.]

Consider a spherical shell of radius $R$ at temperature $T$. The black body radiation inside it can be considered as an ideal gas of photons with internal energy per unit volume $u=\frac{U}{V}\propto T^4$  and pressure$P=\frac{1}{3}\frac{U}{V}$ . If the shell now undergoes an adiabatic expansion the relation between $T$ and $R$ is 

The power radiated by a black body is $P$ and it radiates maximum energy at wavelength, $\lambda_{0}$. If the temperature of the black body is now changed so that it radiates maximum energy at wavelength $\frac{3}{4} \lambda_{0},$ the power radiated by it becomes $nP$. The value of $n$ is