Umakant Kondapure, Collin Fernandes, Nipun Bhatia, Vikram Bathula and, Ketki Deshpande Solutions for Chapter: Wave Theory of Light, Exercise 2: Critical Thinking

A plane glass slab is kept over various coloured letters. The letter which appears the least raised is,

A ray of light is incident normally on a glass slab of refractive index $\mu$ of thickness $d$ which is at a distance $x$ from the glass. The ray of light takes same time to reach from source to slab and to pass through the slab. The thickness of the slab is,

Light entering an air glass $(\mu=1.5)$ boundary is partly reflected and partly refracted. If the incident and reflected rays are at right angles to each other, the angle of refraction $r$ is given by,

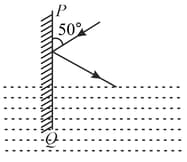
A plane mirror $PQ$ is held normally to water surface of refractive index $1.33$. A ray of light is incident at an angle of $50°$ with the mirror surface. After reflection, the ray is refracted into water. The angle of refraction $r$ is, here $\sin 50°=0.760$.

A ray of light strikes a glass plate at an angle of $60°$. If the reflected and refracted rays are perpendicular to each other, the index of refraction of glass is,

A light source approaches the observer with velocity $0.8 \mathrm{c}$. The Doppler shift for the light of wavelength $5500 \mathrm{\AA }$ is,

Assertion: Contribution of the wavelets lying on back on a wavefront is zero.

Reason: The contribution of a wavelet in any direction making angle $\theta$ with the wavelet is proportional to $\frac{1}{2}(1+\cos \theta)$. In this case, $\theta =180°$.

Assertion: The colour of the light can be assessed from the wavelength of light waves.

Reason: Intensity $=(\text { Amplitude })^{2}$.