D. C. Pandey Solutions for Chapter: Superposition of Waves, Exercise 5: Exercises

A wire with mass $40.0 \mathrm{g}$ is stretched so that its ends are tied down at points $80.0 \mathrm{cm}$ apart. The wire vibrates in its fundamental mode with frequency $60.0 \mathrm{Hz}$ and with an amplitude at the antinodes of $0.300 \mathrm{cm}$.
(a) What is the speed of propagation of transverse wave in the wire?
(b) Compute the tension in the wire.
(c) Find the maximum transverse velocity and acceleration of particles in the wire.

Two harmonic waves are represented in SI units by 
$y_1(x\mathit{,}\mathit{ }t)=0.2\sin (x-3.0t)$ and $y_2(x\mathit{,}\mathit{ }t)=0.2\sin (x-3.0t+\varphi )$
(a) Write the expression for the sum $y=y_1+y_2$ for $\varphi =\frac{\pi }{2} \mathrm{rad}$.
(b) Suppose the phase difference $\varphi$ between the waves is unknown and the amplitude of their sum is $0.32 \mathrm{m}$, what is $\varphi$?

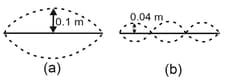
Figure shows different standing wave patterns on a string of linear mass density $4.0\times {10}^{-2} \mathrm{kg} {\mathrm{m}}^{-1}$ under a tension of $100 \mathrm{N}$. The amplitude of antinodes is indicated in each figure. The length of the string is $2.0 \mathrm{m}$.

(i) Obtain the frequencies of the modes shown in figures $\left(\mathrm{a}\right)$ and $\left(\mathrm{b}\right)$.
(ii) Write down the transverse displacement $y$ as a function of $x$ and $t$ for each mode. (Take the initial configuration of the wire in each mode to be as shown by the dark lines in the figure).

A $160 \mathrm{g}$ rope $4 \mathrm{m}$ long is fixed at one end and tied to a light string of the same length at the other end. Its tension is $400 \mathrm{N}$.
(a) What are the wavelengths of the fundamental and the first two overtones?
(b) What are the frequencies of these standing waves?
[Note: In this case, fixed end is a node and the end tied with the light string is antinode.]

A string fastened at both ends has successive resonances with wavelengths of $0.54 \mathrm{m}$ for the $n^{\mathrm{th}}$ harmonic and $0.48 \mathrm{m}$ for the $(n+1{)}^{\mathrm{th}}$ harmonic.
(a) Which harmonics are these?
(b) What is the length of the string?
(c) What is the wavelength of the fundamental frequency?

A wave $y_{\mathit{i}}=0.3 \cos (2.0x-40t)$ is travelling along a string toward a boundary at $x=0$. Write expressions for the reflected waves if
(a) the string has a fixed end at $x=0$ and
(b) the string has a free end at $x=0$
Assume SI units.

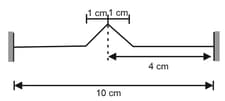
A string that is $10 \mathrm{cm}$ long is fixed at both ends. At $t=0$, a pulse traveling from left to right at $1 \mathrm{cm} {\mathrm{s}}^{-1}$ is $4.0 \mathrm{cm}$ from the right end as shown in figure. Determine the next two times when the pulse will be at that point again. State in each case whether the pulse is upright or inverted.

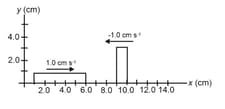
Two pulses travelling in opposite directions along a string are shown for $t=0$ in the figure. Plot the shape of the string at $t=1.0, 2.0, 3.0, 4.0$ and $5.0 \mathrm{s}$, respectively.