The first term of a geometric progression is $1$ and the second term is $2\cos x$, where $0<x<\frac{\pi }{2}$. Find the set of values of $x$ for which this progression is convergent.

A circle of radius $1$ cm is drawn touching the three edges of an equilateral triangle.Three smaller circles are then drawn at each corner to touch the original circle and two edges of the triangle.This process is then repeated an infinite number of times, as shown in the diagram. Find the sum of the circumferences of all the circles. 

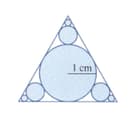
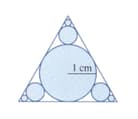
A circle of radius $1$ cm is drawn touching the three edges of an equilateral triangle.Three smaller circles are then drawn at each corner to touch the original circle and two edges of the triangle.This process is then repeated an infinite number of times, as shown in the diagram. Find the sum of the areas of all the circles.

The first term of an Arithmetic progression is $16$ and the second term is $24$ . Find the sum of the first eight terms an Arithmetic progression.

The first term of geometric progression is $16$ and the second term is $24$ . Find the sum of the first eight terms geometric progression.

The first term of a geometric progression is $20$ and second term is $16$ . Find the sum to infinity.

The first term of an Arithmetic progression is $20$ and the second term is $16$ . Find the number of terms in the progression if the sum of all the terms is $-160$.

The first, second and third terms of a geometric progression are the first, fourth and tenth terms, respectively, of an arithmetic progression. Given that the first term in each progression is $12$ and the common ratio of the geometric progression is $r$, where $r\ne 1$, find the value of $r$.

The first, second and third terms of a geometric progression are the first, fourth and tenth terms, respectively, of an arithmetic progression. Given that the first term in each progression is $12$ and the common ratio of the geometric progression is $r$, where $r\ne 1$, find the sixth term of each progression.