HARD
Earn 100
Shown below is a triangular prism of height 10 cm. Calculate its volume.
(Note: Volume = Area of cross section × height.)
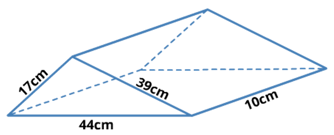
The volume of the prism is
cubic cm.
Shown below is a triangular prism of height 10 cm. Calculate its volume.
(Note: Volume = Area of cross section × height.)

The volume of the prism is cubic cm.
50% studentsanswered this correctly
Important Questions on Heron's Formula
HARD
HARD
EASY
MEDIUM
HARD
EASY
EASY
EASY
HARD
MEDIUM
EASY
MEDIUM
MEDIUM
Find the area of triangle formed by the points and .
EASY
HARD
MEDIUM
Find the area of the triangle formed by joining the middle points of the sides of the triangle whose vertices are and .
HARD
Find the area of the quadrilateral whose vertices are and .
EASY
MEDIUM
Find the area of the triangle formed with the three straight lines represented by:
MEDIUM

