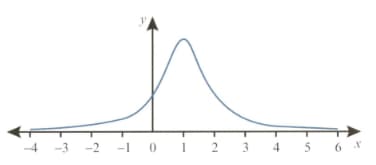
The diagram shows the graph of the probability density function of a variable $X$. Given that the graph is symmetrical about the line $x=1$ and that $P\left(0<X<2\right)=0.6$, find $P\left(X>0\right)$.

$f\left(x\right)=\left\{\begin{array}{l}3e^{-3x} x>0\\ 0 \mathrm{elsewhere}\end{array}\right.$.

The cumulative distribution function of $X$ is

The mean score of $1000$ students for an examination is $34$ and the standard deviation is $16$. Determine the limit of the marks of the central $70\%$ of the candidates by assuming the distribution is normal.

$P\left[0<Z<1.04\right]=0.35$

For the following probability density function (p.d.f) of $X$, $f\left(x\right)=\left\{\begin{array}{ll}\frac{x^2}{18}, & -3<x<3\\ 0,& \mathrm{otherwise}\end{array}\right.$ , find $P(\left|X\right|<1)$.

The value of $K$ for which the probability density function of a variate $X$ is given below.

For the following probability density function (p.d.f) of $X$, $f\left(x\right)=\left\{\begin{array}{ll}\frac{x^2}{18}, & -3<x<3\\ 0,& \mathrm{otherwise}\end{array}\right.$ , find $P(X<1)$.

Which of the following functions is not a p.d.f. (probability density function) of a continuous random variable $x$?

$F_1$ given by

$\begin{array}{c}f\left(x\right)=\left\{\begin{array}{ll}{e}^{-x}& \mathrm{if} 0<x<\infty \\ 0& \mathrm{otherwise}\end{array}\right.\\ \end{array}$

$F_2$ given by

$\begin{array}{c}f\left(x\right)=\left\{\begin{array}{ll}\frac{1}{4}\times \frac{1}{\sqrt{x}}& \mathrm{if} 0<x<4\\ 0& \mathrm{otherwise}\end{array}\right.\\ \end{array}$

$F_3$ given by

$\begin{array}{c}f\left(x\right)=\left\{\begin{array}{ll}6x\left(1-x\right)& \mathrm{if} 0<x<1\\ 0& \mathrm{otherwise}\end{array}\right.\\ \end{array}$

$F_4$ given by

$\begin{array}{c}f\left(x\right)=\left\{\begin{array}{ll}\frac{x}{2}& \mathrm{if} -2<x<2\\ 0& \mathrm{otherwise}\end{array}\right.\\ \end{array}$.

A random variable $X$ has the following probability distribution