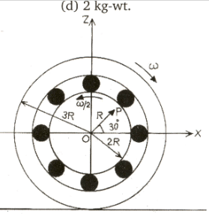
The system in the figure shows a outer ring of radius $3\mathrm{R}$

The figure shows a system consisting of (i) a ring of outer radius $3\mathrm{R}$ rolling clockwise without slipping on a horizontal surface with angular speed $\mathrm{\omega }$ and (ii) an inner disc of radius $2\mathrm{R}$ rotating anti-clockwise with angular speed $\frac{\mathrm{\omega }}{2}$. The ring and disc are separated by frictionless ball bearings. The system is in the $\mathrm{X}-\mathrm{Z}$ plane. The point P on the inner disc is at a distance R from the origin, where OP makes an angle of $30$ degree with the horizontal. Then with respect to the horizontal surface.

A motorcyclist moving with a velocity of $72 \mathrm{km}/\mathrm{hr}$ on a flat road takes a turn on the road at a point where the radius of curvature of the road is $20$ metres. The acceleration due to gravity is $10 {\mathrm{ms}}^{-2}$ in order to avoid skidding, he must not bend with respect to the vertical plane by an angle greater than.

A  bob of mass $\mathrm{m}$ attached to an inextensible string of length $l$ is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed $\mathrm{w} \mathrm{rad}/\mathrm{s}$ about the vertical. About the point of suspension:

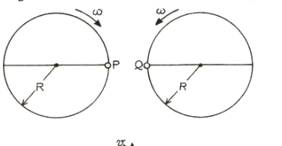
Two identical disc of the same radius are rotating

Two identical discs of same radius $\mathrm{R}$ are rotating about their axes in opposite directions with the same constant angular speed $\mathrm{\varpi }$. The discs are in the same horizontal plane. At time $\mathrm{t}=0$, the points P and Q are facing each other as shown in the figure. The relative speed between the two points P and Q is ${\mathrm{V}}_{\mathrm{r}}$ In one time period (T) of rotation of the discs, ${\mathrm{V}}_{\mathrm{r}}$ as a function of time is best represented by

The limiting value of coefficient of friction between the road and the wheels of a car is $0.5$. The maximum safe speed with which the car can take a bend of radius $5 \mathrm{m}$ on a flat road is nearly 
Take $\mathrm{g}= 9.8 {\mathrm{ms}}^{-2}$.

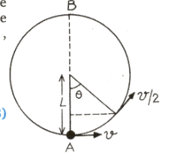
A bob of mass M is suspended by a massless string of length L. The horizontal velocity v at position A is just sufficient to make it reach the point B. The angle $\theta$ at which the speed of the bob is half of that at A, satisfies:

A stone tied to string of length $\mathrm{L}$ is whirled in a vertical circle with the other end of the string at the centre. At a certain instant of time the stone is at its lowest position and has a speed $\mathrm{u}$ The magnitude of the change in velocity as it reaches a position, where the string is horizontal is