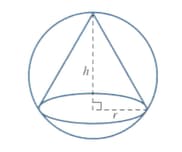
The diagram shows a right circular cone of base radius $r cm$ and height $h cm$ cut from a solid sphere of radius $10 cm$. the volume of the cone is $V c{m}^3$.

Express $r$ in terms of $h$.

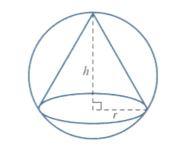
The diagram shows a right circular cone of base radius $r cm$ and height $h cm$ cut from a solid sphere of radius $10 cm$. the volume of the cone is $V c{m}^3$.

Show that $V=\frac{1}{3}\mathrm{\pi }{h}^2\left(20-h\right)$.

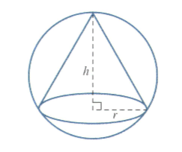
The diagram shows a right circular cone of base radius $r cm$ and height $h cm$ cut from a solid sphere of radius $10 cm$. the volume of the cone is $V c{m}^3$.

Find the value for $h$ for which there is a stationary value of $V$.

The diagram shows a right circular cone of base radius $r cm$ and height $h cm$ cut from a solid sphere of radius $10 cm$. the volume of the cone is $V c{m}^3$.

Find the value for $h$ for which there is a stationary value of $V$.

Determine the magnitude and  nature of this stationary value.

A point is moving along the curve $y=3x-2x^3$ in such a way that the $x-$coordinate is increasing at $0.015$ units per second. Find the rate at which the $y-$coordinate is changing when $x=2$, stating whether the $y-$coordinate is increasing or decreasing.

A point with coordinates $(x, y)$ moves along the curve $y=\sqrt{1+2x}$ in such a way that the rate of increase of $x$ has the constant value $0.01$ units per second. Find the rate of increase of $y$ at the instant when $x=4$..

A point is moving along the curve $y=\frac{8}{x^2-2}$ in such a way that the $x-$coordinate is increasing at a constant rate of $0.005$ units per second. Find the rate of change of the $y-$coordinate as the point passes through the point $(2,4)$.

A point is moving along the curve $y=3\sqrt{x}-\frac{5}{\sqrt{x}}$ in such a way that the $x-$coordinate is increasing at a constant rate of $0.02$ units per second. Find the rate of change of the $y-$coordinate when $x=1$.

A point, $P$, travels along the curve $y=3x+\frac{1}{\sqrt{x}}$ in such a way that the $x-$coordinate of $P$ is increasing at a constant rate of $0.5$ units per second. Find the rate at which the $y-$coordinate of $P$ is changing when $P$ is at the point $(1,4)$.