A stone is catapulted at time , with an initial velocity of magnitude at above the horizontal. What are the magnitudes of the (a) horizontal and
(b) vertical components of its displacement from the catapult site at ? Repeat for the (c) horizontal and (d) vertical components at and for the (e) horizontal and (f) vertical components at

Important Questions on Motion in Two and Three Dimensions
A certain aeroplane has a speed of and is diving at an angle of below the horizontal when the pilot releases a radar decoy in the figure shown below. The horizontal distance between the release point and the point where the decoy strikes the ground is . (a) How long is the decoy in the air? (b) How high was the release point?
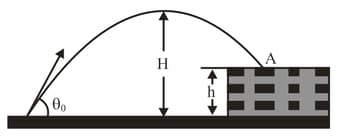
In the figure shown below, a stone is projected at a cliff of height with an initial speed of directed at angle . The stone strikes at , after launching. Find (a) the height of the cliff, (b) the speed of the stone just before impact at , and (c) the maximum height reached above the ground.
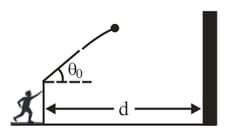
You throw a ball toward a wall at speed and at angle above the horizontal in figure shown below The wall is distance from the release point of the ball.
(a) How far above the release point does the ball hit the wall? What are the (b) horizontal and (c) vertical components of its velocity as it hits the wall? (d) When it hits, has it passed the highest point on its trajectory?
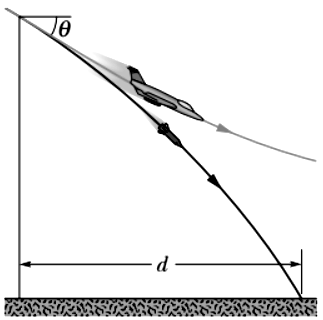
A defense air force plane, diving with constant speed at an angle of with the vertical, drops a shell at an altitude of . The shell reaches the ground after its release.
(a) What is the speed of the plane?
(b) How far does the shell travel horizontally during its flights? What are the
(c) horizontal and
(d) vertical components of its velocity just before reaching the ground? Assume an -axis in the direction of the horizontal motion and an upward -axis.
A trebuchet was a hurling machine built to attack the walls of a castle under siege. A large stone could be hurled against a wall to break apart the wall. The machine was not placed near the wall because the arrows could reach it from the castle wall. Instead, it was positioned, so that, the stone hit the wall during the second half of its flight. Suppose a stone is launched with a speed of and at an angle of . What is the speed of the stone if it hits the wall
(a) Just as it reaches the top of its parabolic path and
(b) when it has descended to half that height?
(c) As a percentage, how much faster is it moving in part (b) than in part (a)?
