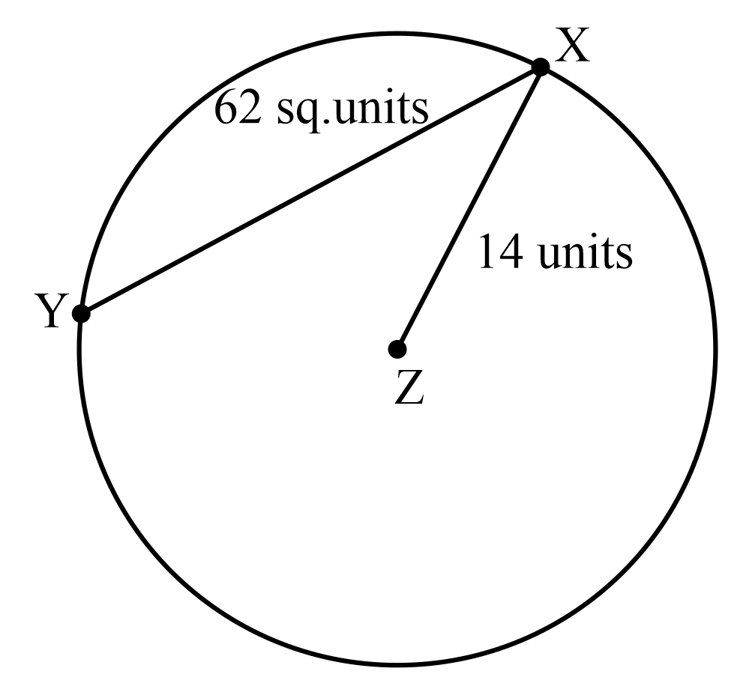
Find the area of the major segment of a circle if the area of the corresponding minor segment is $62 \mathrm{sq}. \mathrm{units}$ and the radius is $14$units. Use $\mathrm{\pi }=\frac{22}{7}$ and write the answer in $\mathrm{sq}. \mathrm{units}$.

Consider the following to the question that follow:

A chord of length $l$ of a circle makes an angle ${90}^{\mathrm{o}}$ at the centre of the circle.

What is the area of the minor segment?

Let $A_1, A_2$ and $A_3$ be the regions on $R^2$ defined by

$A_1=\left\{\left(x,y\right):x\ge 0,y\ge 0,2x+2y-x^2-y^2>1>x+y\right\}$

$A_2=\left\{\left(x,y\right):x\ge 0,y\ge 0,x+y>1>x^2+y^2\right\}$

$A_3=\left\{\left(x,y\right):x\ge 0,y\ge 0,x+y>1>x^3+y^3\right\}$

Denote by $\left|A_1\right|, \left|A_2\right|$ and $\left|A_3\right|$ the areas of the regions $A_1, A_2$ and $A_3$ respectively. Then

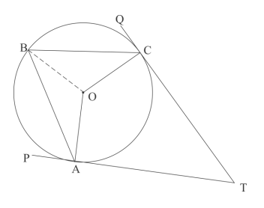
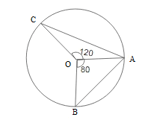
In the given figure $TP$ and $TQ$ are two tangents to the circle with centre $O$, touching at $A$ and $C$ respectively. If $\angle BCQ=55°$ and $\angle BAP=60°$, find$\angle AOC.$

Let $AB$ be a sector of a circle with centre $O$ and radius $d.\angle AOB=\theta \left(<\frac{\pi }{2}\right)$ and $D$ be a point on $OA$ such that $BD$ is perpendicular$OA$. Let $E$ be the mid-point of $BD$ and $F$ be a point on the arc $AB$ such that $EF$ is parallel to $OA$. Then, the ratio of length of the arc$AF$ to the length of the arc $AB$ is

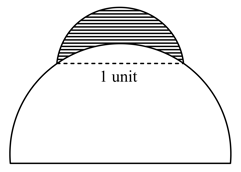
A semi - circle of diameter $1$ unit sits at the top of a semi-circle of diameter $2$ units. The shaded region inside the smaller semi-circle but outside the larger semi-circle is called a lune . The area of the lune is -

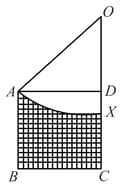
In the figure, $ABCD$ is a unit square. A circle is drawn with centre $O$ on the extended line $CD$ and passing through $A.$ If the diagonal $AC$ is tangent to the circle, then the area of the shaded region is

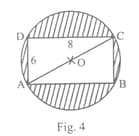
Find the area of shaded region in Fig.$4$, if $ABCD$ is a rectangle with sides $8 cm$ and $6cm$ and $O$ o is the centre of circle $\left(Take \pi =3.14\right)$

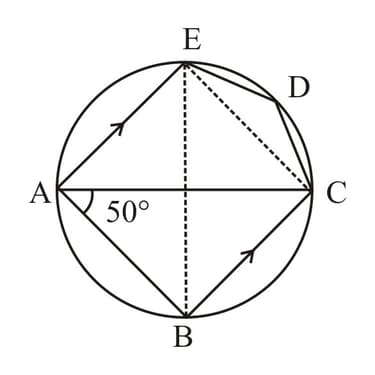
In the given figure, $ABCDE$ is a pentagon inscribed in a circle such that $AC$ is a diameter and side $BC\parallel AE$. If $\angle BAC=50°$, find giving reason

$\angle BEC$

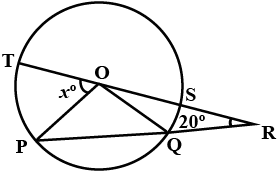
In the figure given below $O$ is the centre of the circle. If the $QR=OP$ and angle $\angle ORP=20°$. Find the value of $x$ giving reasons.

Consider the following to the question that follow:

A chord of length $l$ of a circle makes an angle ${90}^{\mathrm{o}}$ at the centre of the circle.

What is the area of the major segment?

A circular sheet of paper is divided into two sectors. The central angle of one of them is $160°$. These sectors are bent into cones of maximum volume. If the radius of the small cone is $8 \mathrm{cm}$, what is the slant height of the cones in $\mathrm{cm}$?