$A, B$ and $C$ are independent events, and it is given that $\mathrm{P}(A\cap B)=0.35$, $\mathrm{P}(B\cap C)=0.56$ and $\mathrm{P}(A\cap C)=0.4$.

Express $\mathrm{P}\left(A\right)$ in terms of $\mathrm{P}\left(B\right)$.

$A, B$ and $C$ are independent events, and it is given that $\mathrm{P}(A\cap B)=0.35$, $\mathrm{P}(B\cap C)=0.56$ and $\mathrm{P}(A\cap C)=0.4$.

Express $\mathrm{P}\left(A\right)$ in terms of $\mathrm{P}\left(C\right).$

$A, B$ and $C$ are independent events, and it is given that $\mathrm{P}(A\cap B)=0.35$, $\mathrm{P}(B\cap C)=0.56$ and $\mathrm{P}(A\cap C)=0.4$.

Find $\mathrm{P}\left(B\right)$.

$A, B$ and $C$ are independent events, and it is given that $\mathrm{P}(A\cap B)=0.35$, $\mathrm{P}(B\cap C)=0.56$ and $\mathrm{P}(A\cap C)=0.4$.

Find $\mathrm{P}\left(A^{\text{'}}\right)$.

$A, B$ and $C$ are independent events, and it is given that $\mathrm{P}(A\cap B)=0.35$, $\mathrm{P}(B\cap C)=0.56$ and $\mathrm{P}(A\cap C)=0.4$.

Find $\mathrm{P}\left({\mathrm{B}}^{\text{'}}\cap {\mathrm{C}}^{\text{'}}\right)$.

In a class of $28$ children, $19$ attend drama classes, $13$ attend singing lessons, and six attend both drama classes and singing lessons. One child is chosen at random from the class. Event $D$ is 'a child who attends drama classes is chosen. Event $S$ is 'a child who attends singing lessons is chosen.

Illustrate the data in an appropriate diagram.

In a class of $28$ children, $19$ attend drama classes, $13$ attend singing lessons, and six attend both drama classes and singing lessons. One child is chosen at random from the class.
Event $D$ is 'a child who attends drama classes is chosen'.
Event $S$ is 'a child who attends singing lessons is chosen'.

Are events $D$ and $S$ independent? Give a reason for your answer.

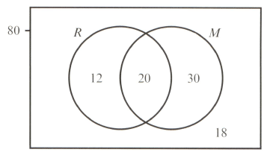
Each child in a group of $80$ was asked whether they regularly read $\left(R\right)$ or regularly watch a movie $\left(M\right)$ The results are given in the Venn diagram opposite. One child is selected at random from the group. Event $R$ is 'a child who regularly reads is selected' and event $M$ is 'a child who regularly watches a movie is selected'.

Determine, with justification, whether events $R$ and $M$ are independent.

Two fair $4$-sided dice, both with faces marked $1, 2, 3$ and $4,$ are rolled.
Event $A$ is 'the sum of the numbers obtained is a prime number'.
Event $B$ is 'the product of the numbers obtained is an even number'

Find, in simplest form, the value of $\mathrm{P}\left(A\right)$, of $\mathrm{P}\left(B\right)$ and of $\mathrm{P}(A\cap B)$.