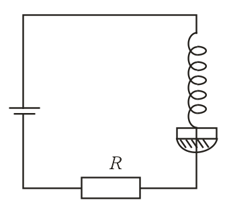
A "dancing spiral" is sometimes demonstrated al lectures. A spring fixed at its upper end is submerged by its lower end into mercury. Voltage supplied by a DC source is applied to the upper end and the mercury. When current flows in the spring, the rings of the spring tend to draw together, the spring gets shorter, and the lower end moves out of the mercury. The current ceases, and the lower end is again submerged in the mercury. The process repeats itself. What oscillations does the spring perform in the process: free, forced, damped, or self-oscillations?

                

Which of the two diagrams, Figures, represents the dependence of the amplitude of displacements in forced oscillations on the frequency of the driving force and which represents the frequency dependence of the velocity amplitude? In what parameter determining the oscillation conditions does each curve represented in Figures differ? What parameters determine the intersection of each curve with the vertical axis in Figure and the position of the maximum?

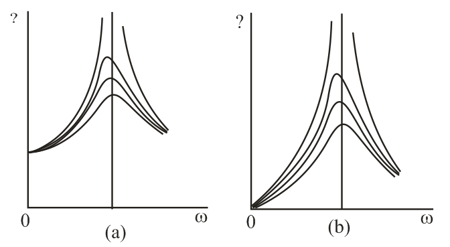
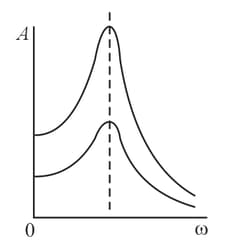
The curve depicting the dependence of the amplitude of forced oscillations on the frequency of the driving force in a medium with no resistance tends to infinity as $\omega ={\omega }_0$. Why is this situation meaningless not only from the physical standpoint but also from the mathematical standpoint? How does a system oscillate in a medium that has practically no resistance?

Two forced oscillations with the same natural frequencies have amplitudes that differ by a factor of $2$ for all values of the frequency of the driving force. In what parameter, among the amplitude of the driving force, the mass of the oscillating object, the elasticity coefficient, and the resistance of the medium, do these systems differ? It is assumed that these systems may differ only in one parameter.

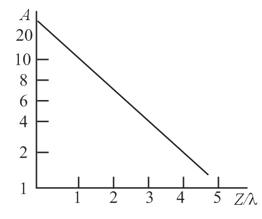
A wave is propagating in a medium with damping. The distance from the source of oscillations (in units of the wavelength) is laid off on the horizontal axis and the common logarithm of the oscillation amplitude is laid off on the vertical axis. Using the graph shown in the figure accompanying the problem, write a formula that will link the amplitude with the distance.

The formula that expresses the speed of sound in a gas can be written in the following form:

$c=\sqrt{\frac{\gamma p}{\rho }}$

Here $\gamma$ is the specific heat ratio (the ratio of the specific heat capacity of the gas at constant pressure to the specific heat capacity at constant volume), $p$ is the pressure of the gas, and $\rho$ is the density of the gas. Using this formula as a basis, can we stipulate that upon isothermal change of the state the speed of sound in the gas grows with pressure?