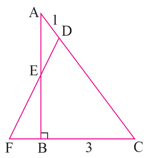
A is a cevian that divides the opposite side into two congruent lengths.
Important Questions on Geometry
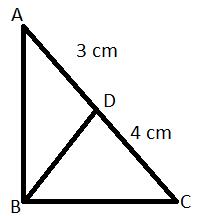
In the triangle , is a cevian. The area of is . Find the area of ,
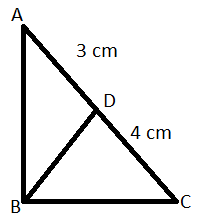
In the triangle , is a cevian. The area of is . Find the area of ,
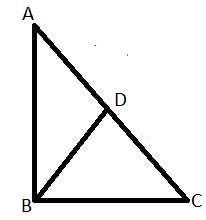
In the triangle , is a cevian. The area of is and is. If the length of is . Find .
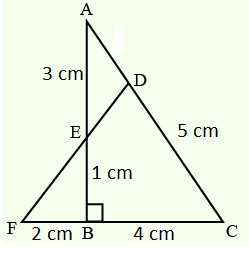
In triangle , points are on the side lines respectively and the points are collinear. Find .
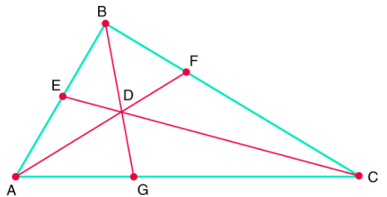
The cevians and of the triangle intersect at . and . Find .
The cevians and of the triangle intersect at . and . Find .
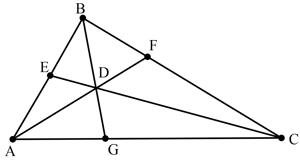
In triangle , points are on the side lines respectively and the points are collinear. Find .
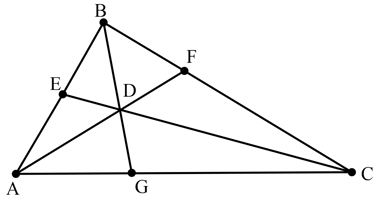
The cevians and of the triangle intersect at . and . Find .
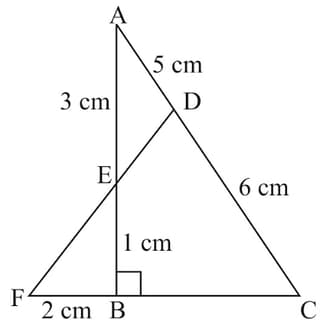
In triangle , points are on the side lines respectively and the points are collinear. Find .
In a garden containing several trees, three particular trees are located in the following way, where are points such that lies on lies on and lies on . Check whether the trees lie on a same straight line.
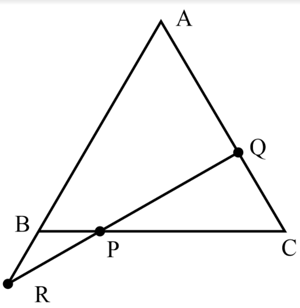
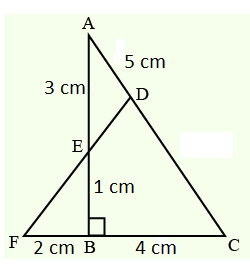
In the given figure, is a triangle with , and . is point on such that and is the midpoint of . Join and and extend to meet at . Find .