A ball of mass is suspended by a thread of length . With what minimum velocity has the point of suspension to be shifted in the horizontal direction for the ball to move along the circle about that point? What will be the tension of the thread at the moment it will be passing the horizontal position?

Important Questions on PHYSICAL FUNDAMENTALS OF MECHANICS
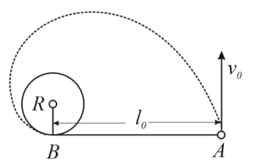
A horizontal plane supports a stationary vertical cylinder of radius and a disc attached to the cylinder by a horizontal thread of length ( top view). An initial velocity , is imparted to the disc as shown in the figure. How long will it move along the plane until it strikes against the cylinder? The friction is assumed to be absent.
A smooth rubber cord of length , whose coefficient of elasticity is , is suspended by one end from the point . The other end is fitted with a catch . A small sleeve of mass starts falling from the point . Neglecting the masses of the thread and the catch, find the maximum elongation of the cord.
A small bar resting on a smooth horizontal plane is attached by threads to a point , and by means of a weightless pulley, to a weight possessing the same mass as the bar itself.
Besides, the bar is also attached to a point by means of a light non-deformed spring of length , and stiffness , where is the mass of the bar. The thread having been burnt, the bar starts moving. Find its velocity at the moment when it is breaking off the plane.
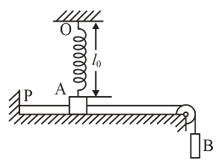
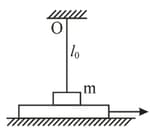
A horizontal plane supports a plank with a bar of mass placed on it and attached by a light elastic non-deformed cord of length to a point . The coefficient of friction between the bar and the plank equals . The plank is slowly shifted to the right until the bar starts sliding over it. It occurs at the moment when the cord deviates from the vertical by an angle . Find the work that has been performed by that moment by the friction force acting on the bar in the reference frame fixed to the plane.
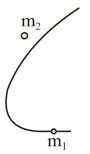
Two interacting particles form a closed system whose centre of inertia is at rest. It illustrates the positions of both the particles at a certain moment and the trajectory of the particle of mass . Draw the trajectory of the particle of mass if .
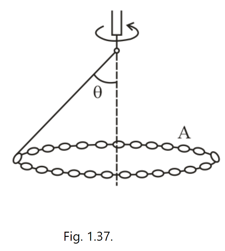
A closed chain of mass is attached to a vertical rotating shaft by means of a thread, and rotates with a constant angular velocity . The thread forms an angle with the vertical. Find the distance between the chain's centre of gravity and the rotation axis, and the tension of the thread.