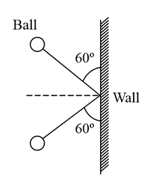
A ball of mass $m$ strikes a rigid wall with speed $u$ at an angle of $30°$ with the normal and gets reflected with the same speed and at the same angle, as shown in the figure. If the ball is in contact with the wall for time $t$, then the force experienced by the wall is:

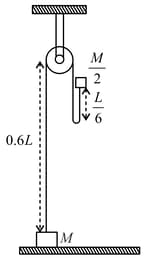
A block of mass $M$ at rest on the floor is attached to a ball of mass $\frac{M}{2}$ via a light inextensible string of length $L$ which passes over a light small frictionless pulley. The pulley is at a height of $0.6 L$ from the floor. The ball is raised to a height of $\frac{L}{6}$  and released (see figure). The speed of the block at the instant the string gets taut (not slack) will be

A rigid ball of mass, $m$ strikes a rigid wall at ${60}^o$ and gets reflected without any loss of speed as shown in the figure below. The value of impulse imparted by the wall on the ball will be


 

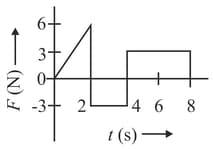
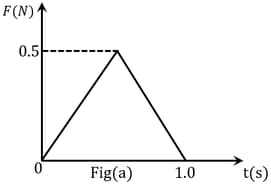
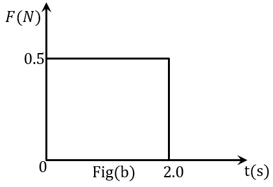
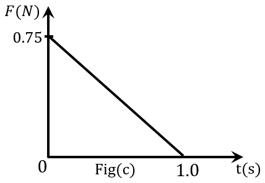
Figures (a), (b), (c) and (d) show variation of force with time.

The impulse is highest in figure.

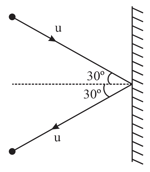
Two billiard balls of equal mass $30 \mathrm{g}$ strike a rigid wall with same speed of $108 \mathrm{km} {\mathrm{h}}^{-1}$ (as shown) but at different angles. If the balls get reflected with the same speed, then the ratio of the magnitude of impulses imparted to ball $a$ and ball $b$ by the wall along $X$ direction is:

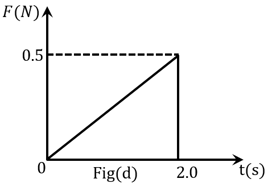
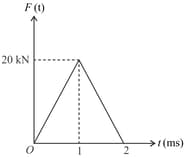
A time varying force acts on a ball of mass $100 \mathrm{g}$ for $2 \mathrm{ms}$. The force versus time curve is shown below. If the initial speed of the ball is $10 \mathrm{m} {\mathrm{s}}^{-1}$, then the speed of ball after $2 \mathrm{ms}$ is

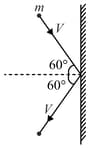
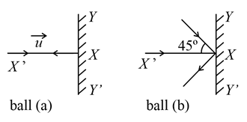
A ball of mass $3 \mathrm{kg}$, moving with a speed of $100 \mathrm{m} {\mathrm{s}}^{-1}$, strikes a wall at an angle $60°$ (as shown in figure). The ball rebounds at the same speed and remains in contact with the wall for $0.2 \mathrm{s}$; the force exerted by the ball on the wall is:

The correct dimensional formula for impulse is given by

Two similar trucks are moving with the same velocity on a road. One of them is loaded while the other is empty. Which of the two will require a larger force to stop it?

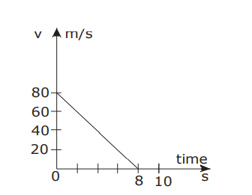
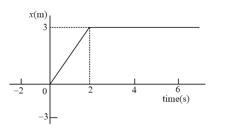
Figure represents the position-time graph of a body of mass $4 \mathrm{kg}$. Impulse $\left(\mathrm{kg} \mathrm{m} {\mathrm{s}}^{-1}\right)$ imparted to the body at $t=0$ is

The force $‘F\text{'}$ acting on a particle of mass $‘m\text{'}$ is indicated by the force-time graph shown below. The change in momentum of the particle over the time interval from zero to $8 \mathrm{s}$ is: