A bar of mass $m$ is held as shown between $4$ disks, each of mass $M \mathrm{and} \mathrm{radius} r=75 \mathrm{mm}$. Determine the acceleration of the bar immediately after it has been released from rest, knowing that the normal forces exerted on the disks are sufficient to prevent any slipping and assuming that; In (i) case, the discs are attached to the fixed support on wall. In (ii) case, the discs are attached to the bar.

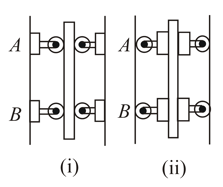
(a) $m=5 \mathrm{kg} \mathrm{and} M=2 \mathrm{kg}$.

(b) the mass of $M$ of the disks is negligible.

(c) the mass of $m$ of the bar is negligible.

Two thin circular discs of mass $2 \mathrm{kg}$ and radius $10 \mathrm{cm}$ each are joined by a rigid massless rod of length $20 \mathrm{cm}$. The axis of the rod is along the perpendicular to the planes of the disk through their centres. This object is kept on a truck in such a way that the axis of the object is horizontal and perpendicular to the direction of motion of the truck. The friction with the floor of the truck is large enough, so that object can roll on the truck without slipping. Take $x$-axis as the direction of motion of the truck and $z$-axis as the vertically upward direction. If the truck has an acceleration of $9 \mathrm{m} {\mathrm{s}}^{-2}$, calculate

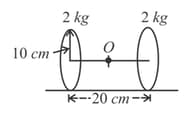
(a) the force of friction on each disc.

(b) the magnitude and direction of frictional torque acting on each disk about the centre of mass $\mathrm{O}$

A rectangular rigid fixed block has a long horizontal edge. A solid homogeneous cylinder of radius $\mathrm{r}$ is placed horizontally at rest with its length parallel to the edge such that the axis of the cylinder and the edge of the block are in the same vertical plane. There is sufficient friction present at the edge so that a very small displacement causes the cylinder to roll off the edge without slipping. Determine : 

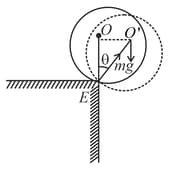
(a) The angle ${\mathrm{\theta }}_{\mathrm{c}}$ through which the cylinder rotates before it leaves contact with the edge.

(b) The speed of the centre of mass of the cylinder before leaving contact with the edge.

(c) The ratio of translational to rotational kinetic energies of the cylinder when its centre of mass is in horizontal line with the edge.

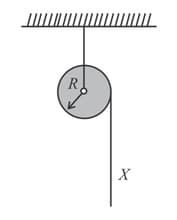
A uniform cylinder of radius $R$ and mass $M$ can rotate freely about a stationary horizontal axis $O$. A thin cord of length $l$ and mass $m$ is wound on the cylinder in a single layer. Find the angular acceleration of the cylinder as a function of the length $x$ of the hanging part of the cord. The wound part of the cord is supposed to have its centre of gravity on the cylinder axis.

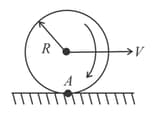
A point $\mathrm{A}$is located on the rim of a wheel of radius $\mathrm{R} = 0.50 \mathrm{m}$ which rolls without slipping along a horizontal surface with velocity $\mathrm{v} = 1.00 \mathrm{m}/\mathrm{s}$ as shown in figure. Find:

(a) the modulus and the direction of the acceleration vector of the point $\mathrm{A}$ ;

(b) the total distance s traversed by the point $\mathrm{A}$ between the two successive moments at which it touches the surface.