A biased die in the shape of a pyramid has five faces marked $1, 2, 3, 4$ and $5$ . The possible scores are $1, 2, 3, 4$ and $5$ and $\mathrm{P}\left(\mathrm{x}\right)=\frac{k-x}{25}$, where $k$ is a constant.

The die is rolled three times and the scores are added together. Evaluate $k$ and find the probability that the sum of the three scores is less than $5$ .

A game board is shown in the diagram.

Players take turns to roll an ordinary fair die, then move their counters forward from 'start' a number of squares equal to the number rolled with the die. If a player's counter ends its move on a coloured square, then it is moved back to the start.

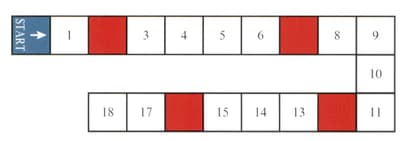
Find the probability that a player's counter is on 'start' after rolling the die once.

A game board is shown in the diagram.

Players take turns to roll an ordinary fair die, then move their counters forward from 'start' a number of squares equal to the number rolled with the die. If a player's counter ends its move on a coloured square, then it is moved back to the start.

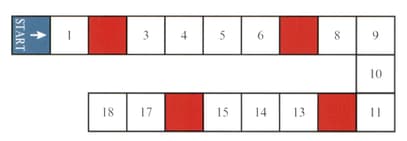
Find the probability that a player's counter is on 'start' after rolling the die twice.

A game board is shown in the diagram.

Players take turns to roll an ordinary fair die, then move their counters forward from 'start' a number of squares equal to the number rolled with the die. If a player's counter ends its move on a coloured square, then it is moved back to the start.

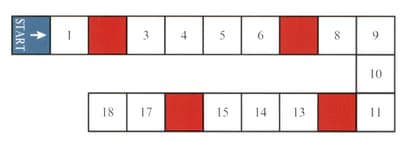
Find the probability that after rolling the die three times, a player's counter is on $18$.

A game board is shown in the diagram.

Players take turns to roll an ordinary fair die, then move their counters forward from 'start' a number of squares equal to the number rolled with the die. If a player's counter ends its move on a coloured square, then it is moved back to the start.

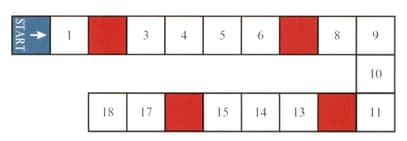
Find the probability that after rolling the die three times, a player's counter is on $17$.

Independent events $S$ and $T$ are such that $\mathrm{P}\left(S\right)=0.4$ and $\mathrm{P}\left(T^{\text{'}}\right)=0.2$. Find:

$\mathrm{P}(S\cap T)$

Independent events $S$ and $T$ are such that $\mathrm{P}\left(S\right)=0.4$ and $\mathrm{P}\left(T^{\text{'}}\right)=0.2$. Find:

$\mathrm{P}\left(S^{\text{'}}\cap T\right).$