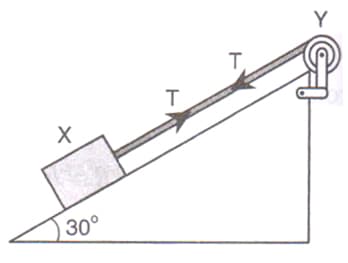
A block of mass is held by a long massless string on a frictionless inclined plane of inclination to the horizontal. The string is wound on a uniform solid cylindrical drum of mass and radius as shown in the diagram. The drum is given an initial angular velocity such that the block starts moving up the plane. Find the tension in the string during motion. At a certain instant of time, the magnitude of the angular velocity of is . Calculate the distance travelled by from that instant of time unit it comes to rest.

Important Questions on Systems of Particles and Rotational Motion
One end of a rod of length is fixed to a point on the circumference of a wheel of radius The other end is sliding freely along a straight channel passing through the center of the wheel as shown in the figure below. The wheel is rotating with a constant angular velocity (in radian per second) about
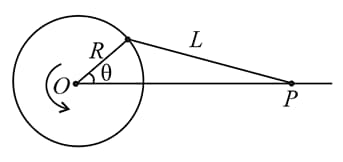
The speed of the sliding end when is
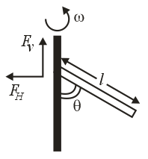
A uniform rod of length ' is pivoted at one of its ends on a vertical shaft of negligible radius. When the shaft rotates at angular speed the rod makes an angle with it (see figure). To find equate the rate of change of angular momentum (direction going into the paper) about the centre of mass (CM) to the torque provided by the horizontal and vertical forces and about the CM. The value of is then such that:
A ball is rolling without slipping in a spherical shallow bowl (radius ) as shown in the figure and is executing simple harmonic motion. If the radius of the ball is doubled, then the time period of oscillation
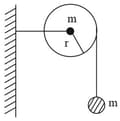
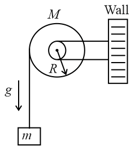
As shown in the figure, a bob of mass is tied to a massless string whose other end portion is wound on a fly wheel (disc) of radius and mass When released from rest the bob starts falling vertically. When it has covered a distance of the angular speed of the wheel will be:

