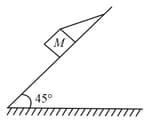
A block of mass $15\mathrm{kg}$ is resting on a rough inclined plane as shown in figure. The block is tied up by a horizontal string which has a tension of $50\mathrm{N}$. Calculate the coefficient of friction between the block and inclined plane.

 

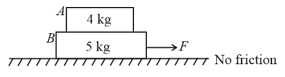
$12\mathrm{N}$ of force required to be applied on $A$ to slip on $B$. Find the maximum horizontal force $F$ to be applied on $B$ so that $A$ and $B$ moves together.

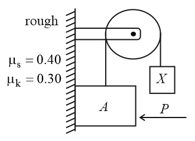
Block $A$ of mass $6\mathrm{kg}$ and block $X$ are attached to a rope which passes over a pulley. A force $P=50\mathrm{N}$ is applied horizontally to block $A$, keeping it in contact with a rough vertical face. The coefficients of static and kinetic friction are ${\mu }_S=0.40$ and ${\mu }_K=0.30$. The pulley is light and  frictionless. In figure, the mass of block $X$ is set so that block $A$ is on the verge of slipping upward. The mass of block $X$ is .......$\mathrm{kg}$.

The block has mass $M$ and rests on a surface for which the coefficients of static and kinetic friction are ${\mu }_s$ and ${\mu }_k$ respectively. A force $F=k{t}^2$ is applied to the cable. Velocity of block at $t=2 \sec$ is $v \mathrm{m} {\mathrm{s}}^{-1}$. Then value of $\frac{23}{v}$ is  Given: $M=24 \mathrm{kg}, k=60 \mathrm{N} {\mathrm{s}}^{-2}, {\mu }_s=0.5, {\mu }_k=0.4$

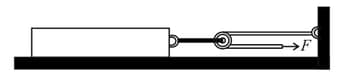
The coefficient of static and kinetic friction between the two blocks and also between the lower block and the ground are ${\mu }_s=0.6$ and ${\mu }_k=0.4$. Find the value of tension $T$ applied on the lower block at which the upper block begins to slip relative to lower block.

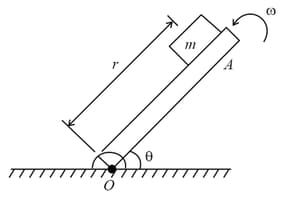
The member $OA$ rotates in vertical plane about a horizontal axis through $O$ with a constant counter clockwise velocity $\omega =3 \mathrm{rad} {\mathrm{s}}^{-1}$. As it passes the position $\theta =0$, a small mass $m$ is placed upon it at a radial distance $r=0.5\mathrm{m}$. If the mass is observed to slip at $\theta =37°$, find the coefficient of friction between the mass & the member.