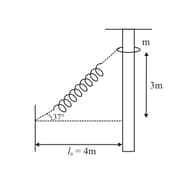
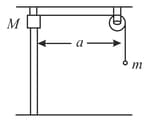
A block of mass $m$ is released from the point $\left(A\right)$ in the figure. The track is frictionless except for the portion between points $\left(B\right)$ and $\left(C\right)$, which has a length of $d_{\mathrm{BC}}$. The block travels down the track, hits a spring of force constant $k$, and compresses the spring $x$ from its equilibrium position before coming to rest momentarily. Determine the coefficient of kinetic friction between the block and the rough surface between $\left(B\right)$ and $\left(C\right)$.

 

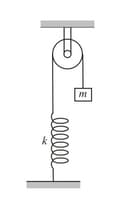
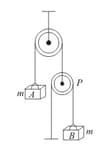
In the figure, the stiffness of the spring is $k$ and the mass of the block is $m$. The pulley is fixed. Initially, the block $m$ is held such that the elongation in the spring is zero and then released from rest.

$\left(\mathrm{a}\right)$ Find the maximum elongation in the spring

$\left(\mathrm{b}\right)$ the maximum speed of the block $m$.

Neglect the mass of the spring and that of the string. Also, neglect the friction.

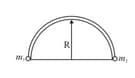
A spring-mass system $\left(m_1+\mathrm{massless} \mathrm{spring}+m_2\right)$ fall freely from a height $h$ before $m_2$ colliding inelastically with the ground. Find the maximum value of $h$ so that block $m_2$ will break off the surface. Assume $k=$ stiffness of the spring.

In an ideal pulley particle system, the mass $m_2$ is connected with a vertical spring of stiffness $k$. If the mass $m_2$ is released from rest, when the spring is deformed, find the maximum compression of the spring.

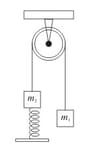
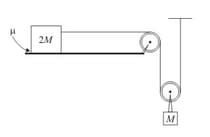
The figure below shows two blocks of masses $2M$ and $M$, respectively. The coefficient of friction between the block of mass $2M$ and the horizontal plane is $\mu$. The system is released from rest. Find the velocity of the block of mass $M$, when the block of mass $2M$ has moved a distance $s$ towards the right.