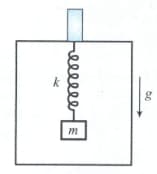
A block of mass $m$ is suspended from the ceiling of a stationary elevator through a spring of spring constant $k$; it is in equilibrium. Suddenly, the cable breaks and the elevator starts falling freely. Show that the block now executes a simple harmonic motion of amplitude $\frac{mg}{k}$ in the elevator.

 

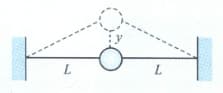
A ball of mass $m$ is connected to two rubber bands of length $L$, each under tension $T$ as shown in the figure. The ball is displaced by a small distance $y$ perpendicular to the length of the rubber bands. Assuming the tension does not change, show that

(a) the restoring force is $-\left(\frac{2\mathrm{T}}{L}\right)y$ and

(b) the system exhibits simple harmonic motion with an angular frequency $\omega =\sqrt{\frac{2\mathrm{T}}{mL}}$.

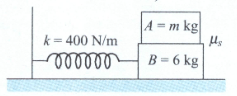
Two blocks lie on each other and are connected to a spring as shown in the figure. What should be the mass of block $A$ placed on block $B$ of mass $6\mathrm{kg}$ so that the system is period is $1\mathrm{s}$. Assuming no slipping, what should be the minimum value of coefficient of static friction $\mu$, for which block $A$ will not slip relative to block $B$, if block $B$ is displaced $50\mathrm{mm}$ from equilibrium position and released?

(Given: $g=10{\mathrm{ms}}^{-2}$ and ${\pi }^2=10$)

The potential energy $\left(U\right)$ of a body of unit mass moving in a one-dimensional conservative force field is given by $U=\left(x^2-4x+3\right)$. All units are in SI unit. Find the equilibrium position of the body.

The potential energy $\left(U\right)$ of a body of unit mass moving in a one-dimensional conservative force field is given by $U=\left(x^2-4x+3\right)$. $U$ and $x$ are in SI units. Show that oscillations of the body about this equilibrium position are in simple harmonic motion and find its time period.

The potential energy $\left(U\right)$ of a body of unit mass moving in a one-dimensional conservative force field is given by $U=\left(x^2-4x+3\right)$. All units are in SI. Find the amplitude of oscillations if the speed of the body at equilibrium position is $2\sqrt{6} \mathrm{m} {\mathrm{s}}^{-1}$.